【题目】如图,已知PA、PB切⊙O于A,B两点,连AB,且PA,PB的长是方程x2﹣2mx+3=0的两根,AB=m.试求: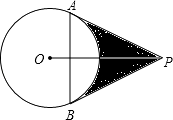
(1)⊙O的半径;
(2)由PA,PB, ![]() 围成图形(即阴影部分)的面积.
围成图形(即阴影部分)的面积.
参考答案:
【答案】
(1)解:连OA,OB,

∵PA=PB,
∴△=(﹣2m)2﹣4×3=0,
∴m2=3,m>0,
∴m= ![]() ,
,
∴x2﹣2 ![]() x+3=0,
x+3=0,
∴x1=x2= ![]() ,
,
∴PA=PB=AB= ![]() ,
,
∴△ABP等边三角形,
∴∠APB=60°,
∴∠APO=30°,
∵PA= ![]() ,
,
∴OA=1
(2)解:∵∠AOP=60°,
∴∠AOB=120°,
S阴=S四边形OAPB﹣S扇形OAB
=2S△AOP﹣S扇形OAB
=2× ![]() ×1×
×1× ![]() ﹣
﹣ ![]() ,
,
= ![]() ﹣
﹣ ![]() π.
π.
【解析】(1)由已知易证PA=PA,而PA、PB是一元二次方程的两个根,可知一元二次方程由两个相等的实数根,根据b2-4ac=0,建立方程,即可求出m的值,再证明△ABP等边三角形,就可求出圆的半径长。
(2)观察图形S阴=2S△AOP﹣S扇形OAB,分别求出△AOP和扇形OAB的面积即可。
【考点精析】掌握公式法和求根公式是解答本题的根本,需要知道要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之;根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1的图形我们把它称为“8字形”,则∠A,∠B,∠C,∠D四个角的数量关系是 ;
(2)如图2,若∠BCD,∠ADE的角平分线CP,DP交于点P,则∠P与∠A,∠B的数量关系为∠P= ;
(3)如图3,CM,DN分别平分∠BCD,∠ADE,当∠A+∠B=80°时,试求∠M+∠N的度数(提醒:解决此问题可以直接利用上述结论);
(4)如图4,如果∠MCD=
 ∠BCD,∠NDE=
∠BCD,∠NDE= ∠ADE,当∠A+∠B=n°时,试求∠M+∠N的度数.
∠ADE,当∠A+∠B=n°时,试求∠M+∠N的度数.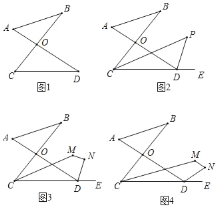
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)

(1)求这条抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在说明理由; -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=
 ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( ) 
A.
B.2
C.3
D.2
-
科目: 来源: 题型:
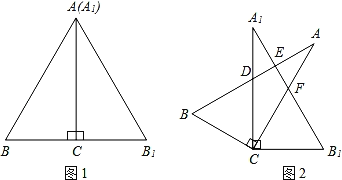
查看答案和解析>>【题目】将两块全等的含30°角的直角三角扳按图1的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转(如图2所示),AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.给出下列结论:
①当旋转角等于20°时,∠BCB1=l60°;
②当旋转角等于30°时,AB与A1B1垂直;
③当旋转角等于45°时,AB∥CB1;
④当AB∥CB1时,点D为A1C的中点.
其中正确的是_____(写出所有正确结论的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠ABC=3∠C,∠BAC的平分线AD交BC于D,BE⊥AD于E.
(1)如图l,求证:AC﹣AB=2BE.
(2)如图2,将∠DCA沿直线AC翻折,交BA的延长线于点M,连接MD交AC于点N;MA=BA,BE=1,AB=
 ,求AN的长.
,求AN的长.
相关试题

