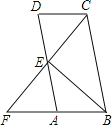
【题目】如图,已知平行四边形ABCD中,E为AD中点,CE延长线交BA延长线于点F.
(1)求证:CD=AF;
(2)若BC=2CD,求证:∠F=∠BCF
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)CD和AF分别在△DCE和△AFE中,要证它们相等,只需证△DCE≌△AFE,根据平行四边形的性质及E为AD中点可证.
(2)在平行四边形中,对边相等,由(1)的结论可证昨BF=BC,根据等边对等角可证.
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DC.
∴∠DCE=∠AFE.
∵E是AD的中点,
∴DE=AE.
在△DCE和△AFE中
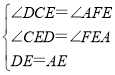 ,
,
∴△DCE≌△AFE.
∴CD=AF.
(2)由(1)得CD=AF,
∵AB=CD,
∴BF=AF+AB=2CD.
∵BC=2CD,
∴BF=BC.
∴∠F=∠BCF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,两条对角线AC、BD相交于点O, ∠AOB=60° AB=4cm.则这个矩形的周长是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G、交BC的延长线于H,则以下结论:①DE=DG;②BE=CG;③DF=DB;(④BH=CF.其中正确的是____

-
科目: 来源: 题型:
查看答案和解析>>【题目】为丰富群众的业余生活并迎接社区文艺汇演,某小区特组建了一支“大妈广场舞队”(人数不超过50人).排练时,若排7排,则多3人;若排9排,且每排人数仅比排7 排时少1人,则最后-排不足6人.
(1)该“大妈广场舞队”共有多少名成员?
(2)为了提升表演效果,领队决定购买扇子和鲜花作为“大妈广场舞队”的表演道具.经预算,如果给40%的成员每人配1把扇子,其余的每人配1束鲜花,那么共需花费558元;如果 给60%的成员每人配1把扇子,其余的每人配1束鲜花,那么共需花费612元.问扇子和 鲜花的单价各是多少元?
-
科目: 来源: 题型:
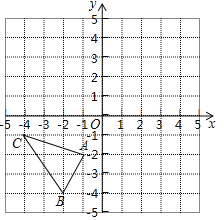
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)把△ABC向上平移3个单位后得到△A1B1C1,请画出△A1B1C1并写出点B1的坐标;
(2)已知点A与点A2(2,1)关于直线l成轴对称,请画出直线l及△ABC关于直线l对称的△A2B2C2,并直接写出直线l的函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(-20)+(-18)-(-14)-13
(2) 8+(-3)×(-2)2
(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题提出):分解因式:(1)2x2+2xy﹣3x﹣3y;(2)a2﹣b2+4a﹣4b
(问题探究):某数学“探究学习”小组对以上因式分解题目进行了如下探究:
探究1:分解因式:(1)2x2+2xy﹣3x﹣3y
该多项式不能直接使用提取公因式法,公式法进行因式分解.于是仔细观察多项式的特点.甲发现该多项式前两项有公因式2x,后两项有公因式﹣3,分别把它们提出来,剩下的是相同因式(x+y),可以继续用提公因式法分解.
解:2x2+2xy﹣3x﹣3y=(2x2+2xy)﹣(3x+3y)=2x(x+y)﹣3(x+y)=(x+y)(2x﹣3)
另:乙发现该多项式的第二项和第四项含有公因式y,第一项和第三项含有公因式x,把y、x提出来,剩下的是相同因式(2x﹣3),可以继续用提公因式法分解.
解:2x2+2xy﹣3x﹣3y=(2x2﹣3x)+(2xy﹣3y)=x(2x﹣3)+y(2x﹣3)=(2x﹣3)(x+y)
探究2:分解因式:(2)a2﹣b2+4a﹣4b
该多项式亦不能直接使用提取公因式法,公式法进行因式分解,于是若将此题按探究1的方法分组,将含有a的项分在一组即a2+4a=a(a+4),含有b的项一组即﹣b2﹣4b=﹣b(b+4),但发现a(a+4)与﹣b(b+4)再没有公因式可提,无法再分解下去.于是再仔细观察发现,若先将a2﹣b2看作一组应用平方差公式,其余两项看作一组,提出公因式4,则可继续再提出因式,从而达到分解因式的目的.
解:a2﹣b2+4a﹣4b=(a2﹣b2)+(4a﹣4b)=(a+b)(a﹣b)+4(a﹣b)=(a﹣b)(4+a+b)
(方法总结):对不能直接使用提取公因式法,公式法进行分解因式的多项式,我们可考虑把被分解的多项式分成若干组,分别按“基本方法”即提取公因式法和运用公式法进行分解,然后,综合起来,再从总体上按“基本方法”继续进行分解,直到分解出最后结果.这种分解因式的方法叫做分组分解法.
分组分解法并不是一种独立的因式分解的方法,而是通过对多项式进行适当的分组,把多项式转化为可以应用“基本方法”分解的结构形式,使之具有公因式,或者符合公式的特点等,从而达到可以利用“基本方法”进行分解因式的目的.
(学以致用):尝试运用分组分解法解答下列问题:
(1)分解因式:
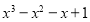
(2)分解因式:

(拓展提升):
(3)尝试运用以上思路分解因式:
相关试题

