【题目】矩形ABCD中,两条对角线AC、BD相交于点O, ∠AOB=60° AB=4cm.则这个矩形的周长是________.
参考答案:
【答案】![]()
【解析】
根据矩形性质得出AD=BC,AB=CD,∠BAD=90°,OA=OC=![]() AC,BO=OD=
AC,BO=OD=![]() BD,AC=BD,推出OA=OB=OC=OD,得出等边三角形AOB,求出BD,根据勾股定理求出AD即可.
BD,AC=BD,推出OA=OB=OC=OD,得出等边三角形AOB,求出BD,根据勾股定理求出AD即可.
解:∵四边形ABCD是矩形,

∴∠BAD=90°,OA=OC=![]() AC,BO=OD=
AC,BO=OD=![]() BD,AC=BD,
BD,AC=BD,
∴OA=OB=OC=OD,
∵∠AOB=60°,OB=OA,
∴△AOB是等边三角形,
∵AB=4,
∴OA=OB=AB=4,
∴BD=2OB=8,
在Rt△BAD中,AB=4,BD=8,由勾股定理得:AD=![]() ,
,
∵四边形ABCD是矩形,
∴AB=CD=4,AD=BC=![]() ,
,
∴矩形ABCD的周长是AB+BC+CD+AD=8+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为开展“校园读书活动”,雅礼中学读书会计划采购数学文化和文学名著两类书籍共100本. 经了解,购买20 本数学文化和50本文学名著共需1700元, 30本数学文化比30本文学名著贵450 元. (注:所采购的同类书籍价格都一样)
(1)求每本数学文化和文学名著的价格;
(2)若校园读书会要求购买数学文化本数不少于文学名著,且总费用不超过2780元,请求出所有符合条件的购书方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张同学在计算
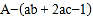 时,将“
时,将“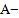 ”错看成了“
”错看成了“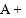 ”,得出的结果是
”,得出的结果是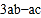 .
.(1)请你求出这道题的正确结果;
(2)试探索:当字母
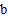 、
、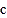 满足什么关系时,(1)中的结果与字母
满足什么关系时,(1)中的结果与字母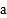 的取值无关.
的取值无关. -
科目: 来源: 题型:
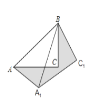
查看答案和解析>>【题目】如图,在△ABC中,AB=6,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1,则阴影部分的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G、交BC的延长线于H,则以下结论:①DE=DG;②BE=CG;③DF=DB;(④BH=CF.其中正确的是____

-
科目: 来源: 题型:
查看答案和解析>>【题目】为丰富群众的业余生活并迎接社区文艺汇演,某小区特组建了一支“大妈广场舞队”(人数不超过50人).排练时,若排7排,则多3人;若排9排,且每排人数仅比排7 排时少1人,则最后-排不足6人.
(1)该“大妈广场舞队”共有多少名成员?
(2)为了提升表演效果,领队决定购买扇子和鲜花作为“大妈广场舞队”的表演道具.经预算,如果给40%的成员每人配1把扇子,其余的每人配1束鲜花,那么共需花费558元;如果 给60%的成员每人配1把扇子,其余的每人配1束鲜花,那么共需花费612元.问扇子和 鲜花的单价各是多少元?
-
科目: 来源: 题型:
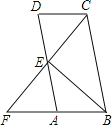
查看答案和解析>>【题目】如图,已知平行四边形ABCD中,E为AD中点,CE延长线交BA延长线于点F.
(1)求证:CD=AF;
(2)若BC=2CD,求证:∠F=∠BCF
相关试题

