【题目】铜仁某校高中一年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次.甲、乙两名同学测试情况如图所示:

![]() 根据图6提供的信息填写下表:
根据图6提供的信息填写下表:
平均数 | 众数 | 方差 | |
甲 |
| ||
乙 |
|
![]() 如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据平均数和众数的定义求解;
(2)根据折线图平均数一样,而乙的众数大,甲的方差小,成绩稳定;故选甲或乙均有道理,只要说理正确即可.
解:(1)据折线图的数据,甲的数据中,6出现的次数最多,故众数是6;
平均数为:![]() (9+6+6+8+7+6+6+8+8+6)=7;
(9+6+6+8+7+6+6+8+8+6)=7;
乙的数据中,8出现的次数最多,故众数是8;
平均数为:![]() (4+5+7+6+8+7+8+8+8+9)=7;
(4+5+7+6+8+7+8+8+8+9)=7;
平均数 | 众数 | 方差 | |
甲 | 7 | 6 |
|
乙 | 7 | 8 |
|
(2)
选甲:平均数与乙一样,甲的方差小于乙的方差,甲的成绩比乙的成绩稳定.
选乙:平均数与甲一样,乙投中篮的众数比甲投中篮的众数大,且从折线图看出,乙比甲潜能更大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
(1)求证:直线EF是⊙O的切线;
(2)若CF=3,cosA=0.4,求出⊙O的半径和BE的长;
(3)连接CG,在(2)的条件下,求CG:EF的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形都是由同样大小的棋子按一定的规律组成,其中第
 个图形有
个图形有 颗棋子,第
颗棋子,第 个图形一共有
个图形一共有 颗棋子,第
颗棋子,第 个图形一共有
个图形一共有 颗棋子,,则第
颗棋子,,则第 个图形中棋子的颗数为( )
个图形中棋子的颗数为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形
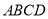 的对角线交于点
的对角线交于点 ,
,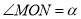 .
.(1)如图1,
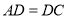 ,
,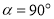 ,点
,点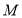 在边
在边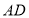 上,点
上,点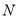 在边
在边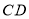 上,求证:
上,求证: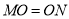 ;
;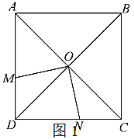
(2)如图2,
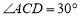 ,
,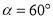 ,点
,点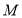 在线段
在线段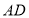 的延长线上,点
的延长线上,点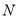 在线段
在线段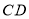 的延长线上,若
的延长线上,若 ,求
,求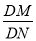 的值;
的值;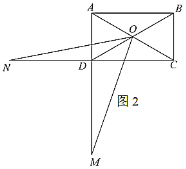
(3)如图3,
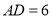 ,
,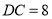 ,
,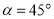 ,点
,点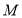 在线段
在线段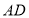 的延长线上,点
的延长线上,点 在线段
在线段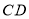 的延长线上,若
的延长线上,若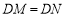 ,直接写出线段
,直接写出线段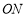 的长度.
的长度.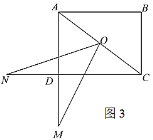
-
科目: 来源: 题型:
查看答案和解析>>【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向
 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
-
科目: 来源: 题型:
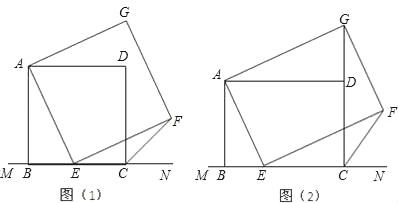
查看答案和解析>>【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.
相关试题

