【题目】为了更好地治理水质,保护环境,我县污水处理公司决定购买10台污水处理设备,现有A、B两种设备可供选择,月处理污水分别为240m3/月、200m3/月,经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)若污水处理公司购买设备的预算资金不超过105万元,你认为该公司有哪几种购买方案?
(2)若每月需处理的污水约2040m3,在不突破资金预算的前提下,为了节约资金,又要保证治污效果,请你为污水处理公司设计一种最省钱的方案.
参考答案:
【答案】(1)购买方案:①A型设备1台,B型设备9台;②A型设备2台,B型设备8台;③A型设备0台,B型设备10台;(2)该公司购买方案A型设备1台,B型设备9台第一种方案最省钱.
【解析】
(1)设每台A型设备和每台B型设备各需要x万元、y万元,由题意得:买一台A型设备的价钱﹣买一台B型设备的价钱=2万元;购买3台B型设备﹣购买2台A型设备比=6万元.根据等量关系列出方程组,解方程组即可;再设应购置A型号的污水处理设备a台,则购置B型号的污水处理设备(10﹣a)台,由于要求资金不能超过105万元,即购买资金12a+10(10﹣a)≤105万元,根据不等关系列出不等式,再解不等式,求出非负整数解即可;
(2)再设应购置A型号的污水处理设备m台,则购置B型号的污水处理设备(10﹣m)台,由于要求资金不能超过105万元,即购买资金12m+10(10﹣m)≤105万元,再根据“每台A型设备每月处理污水240吨,每台B型设备每月处理污水200吨,每月处理的污水不低于2040吨”可得不等关系:240m+200(10﹣m)≥2040吨;把两个不等式组成不等式组,由此求出关于A型号处理机购买的几种方案,分类讨论,选择符合题意得那个方案即可.
(1)设每台A型设备和每台B型设备各需要x万元、y万元,由题意得:
![]() ,
,
解得![]() .
.
设应购置A型号的污水处理设备a台,则购置B型号的污水处理设备(10﹣a)台,
12a+10(10﹣a)≤105,
解得:a≤2.5,
∵a为非负整数,
∴a=0,1,2,
购买方案:①A型设备1台,B型设备9台;②A型设备2台,B型设备8台;③A型设备0台,B型设备10台;
(2)设应购置A型号的污水处理设备m台,则购置B型号的污水处理设备(10﹣m)台,
由题意得:![]() ,
,
解得:1≤m≤2.5,
∵m为整数,
∴m=1,2,
则B型购买的台数依次为9台,8台;
∵A型号的污水处理设备12万元一台,比B型的贵,
∴少买A型,多买B型的最省钱,
故买A型1台,B型9台,
答:该公司购买方案A型设备1台,B型设备9台第一种方案最省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在数轴上表示的数是﹣2,点B表示+6,P、Q两点同时分别以1个单位/秒和3个单位/秒的速度从A、B两点出发,沿数轴规则运动
(1)求线段AB的长度;
(2)如果P、Q两点在数轴上相向移动,问几秒钟后PQ=
 AB?
AB?(3)如果P、Q两点在数轴上同时沿数轴负半轴方向移动(Q在P的左侧),若M、N分别是PA和BQ中点,问是否存在这样的时间t,使得线段MN=
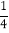 AB?若存在,请求出t的值;若不存在,请说明理由.
AB?若存在,请求出t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平安路与幸福路是两条平行的道路,且都与新兴大街垂直,老街与小米胡同垂直,书店位于老街与小米胡同的交口处.如果小强同学站在平安路与新兴大街交叉路口,准备去书店,按图中的街道行走,最近的路程为( )

A. 300m B. 400m C. 500m D. 700m
-
科目: 来源: 题型:
查看答案和解析>>【题目】北京奥运会期间,某旅行社组团去北京观看某场足球比赛,入住某宾馆.已知该宾馆一楼房间比二楼房间少5间,该旅游团有48人,若全部安排在一楼,每间住4人,房间不够,每间住5人,有房间没住满.若全部安排在二楼,每间住3人,房间不够,每间住4人,则有房间没住满.你能根据以上信息确定宾馆一楼有多少房间吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两名运动员,选择一人参加市射击比赛,在选拔赛上,每人打10发,其中甲的射击成绩分别为10、8、7、9、8、10、10、9、10、9
①计算甲的射击成绩的方差;
②经过计算,乙射击的平均成绩是9,方差为1.4,你认为选谁去参加市射击比赛合适,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是
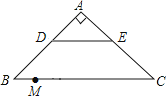
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是;
(2)请用列表法或画树状图(树形图)法求小明和小亮诵读两个不同材料的概率.
相关试题

