【题目】探究题
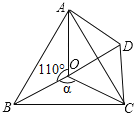
如图,点O是等边△ABC内一点,∠A OB﹦1100,∠BOC﹦a,将△BOC绕点C按顺时钟方向旋转60O得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当a﹦150O时,试判断△AOD的形状,并说明理由;
(3)探究:当仅为多少度时,△AOD是等腰三角形?
参考答案:
【答案】(1)等边三角形;(2)直角三角形;(3)当![]() 的度数为
的度数为![]() 或
或![]() 或
或![]() 时,△AOD是等腰三角形.
时,△AOD是等腰三角形.
【解析】(1)根据旋转的性质可得出OC=OD,结合题意即可证得结论;
(2)结合(1)的结论可作出判断;
(3)找到变化中的不变量,然后利用旋转及全等的性质即可做出解答.
(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC
∴CO=CD,∠OCD=60°
∴△COD是等边三角形.
(2)解:当![]() =150°时,△AOD是直角三角形
=150°时,△AOD是直角三角形
理由是:∵△BOC≌△ADC
∴∠ADC=∠BOC=150°
又∵△COD是等边三角形
∴∠ODC=60°[来
∴∠ADO=∠ADC -∠ODC=90°,即△AOD是直角三角形.
(3)解:①要使AO=AD,需∠AOD=∠ADO
∵∠AOD= ![]() =
= ![]() ,∠ADO=
,∠ADO= ![]()
∴![]() =
= ![]()
∴![]()
②要使OA=OD,需∠OAD=∠ADO
∵∠OAD=![]() (∠AOD+∠ADO)=
(∠AOD+∠ADO)=![]() =
=![]()
∴![]() =
=![]()
∴![]()
③要使DO=DA,需∠OAD=∠AOD.
∵∠AOD= ![]() =
= ![]() ,∠OAD=
,∠OAD=![]() ∴
∴![]() =
=![]() ,解得
,解得![]()
综上所述:当![]() 的度数为
的度数为![]() 或
或![]() 或
或![]() 时,△AOD是等腰三角形.
时,△AOD是等腰三角形.
“点睛”本题以“空间与图形”中的核心知识(如等边三角形)的性质、全等三角形的性质与证明、直角三角形的判定、多边形内角和等)为载体,内容由浅入深,层层递进,试题中几何演绎推理的难度适中,蕴含着丰富的思想方法(如运动变化、数形结合、分类讨论、方程思想等)能较好地考查学生的推理、探究及解决问题的能力.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 某市为更有效地利用水资源,制定了居民用水收费标准:如果一户每月用水量不超过15立方米,每立方米按2.8元收费;如果超过15立方米,超过部分按每立方米3.3元收费.若某户一月份共支付水费58.5元,求该户一月份用水量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016重庆市第18题)如图,在正方形ABCD中,AB=6,点E在边CD上,DE=
 DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是_______.
DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是_______.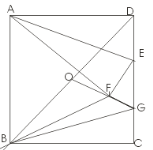
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广东省梅州市第18题)
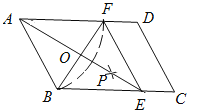
如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于
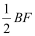 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF. (1)、四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)、AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016贵州省毕节市第25题)如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
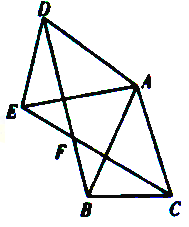
(1)求证:
 ;
;(2)若AB=2,
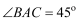 ,当四边形ADFC是菱形时,求BF的长。
,当四边形ADFC是菱形时,求BF的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在解方程
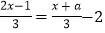 ,去分母时,方程右边的-2没有乘3,因而求得方程的解为x=3.试求a的值,并正确地解出方程.
,去分母时,方程右边的-2没有乘3,因而求得方程的解为x=3.试求a的值,并正确地解出方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广西省贺州市第18题)在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)
相关试题

