【题目】(2016贵州省毕节市第25题)如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
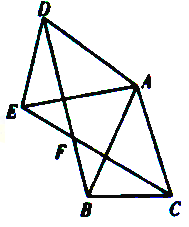
(1)求证:![]() ;
;
(2)若AB=2,![]() ,当四边形ADFC是菱形时,求BF的长。
,当四边形ADFC是菱形时,求BF的长。
参考答案:
【答案】(1)、证明过程见解析;(2)、BF=2![]() -2
-2
【解析】
(2)试题分析:(1)、根据△ABC≌△ADE得出AE=AD,∠BAC=∠DAE,从而得出∠CAE=∠DAB,根据SAS判定定理得出三角形全等;(2)、根据菱形的性质得出∠DBA=∠BAC=45°,根据AB=AD得出△ABD是直角边长为2的等腰直角三角形,从而得出BD=2![]() ,根据菱形的性质得出AD=DF=FC=AC=AB=2,最后根据BF=BD-DF求出答案.
,根据菱形的性质得出AD=DF=FC=AC=AB=2,最后根据BF=BD-DF求出答案.
试题解析:(1)、∵△ABC≌△ADE且AB=AC ∴AE=AD,AB=AC
∠BAC+∠BAE=∠DAE+∠BAE ∴∠CAE=∠DAB ∴△AEC≌△ADB
(3)、∵四边形ADFC是菱形且∠BAC=45° ∴∠DBA=∠BAC=45° 由(1)得AB=AD
∴∠DBA=∠BDA=45° ∴△ABD是直角边长为2的等腰直角三角形 ∴BD=2![]()
又∵四边形ADFC是菱形 ∴AD=DF=FC=AC=AB=2 ∴BF=BD-DF=2![]() -2
-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016重庆市第18题)如图,在正方形ABCD中,AB=6,点E在边CD上,DE=
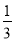 DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是_______.
DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是_______.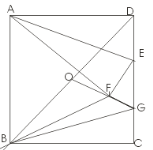
-
科目: 来源: 题型:
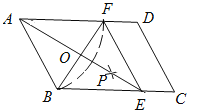
查看答案和解析>>【题目】(2016广东省梅州市第18题)
如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于
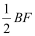 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF. (1)、四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)、AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
-
科目: 来源: 题型:
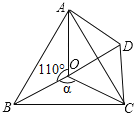
查看答案和解析>>【题目】探究题
如图,点O是等边△ABC内一点,∠A OB﹦1100,∠BOC﹦a,将△BOC绕点C按顺时钟方向旋转60O得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当a﹦150O时,试判断△AOD的形状,并说明理由;
(3)探究:当仅为多少度时,△AOD是等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在解方程
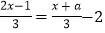 ,去分母时,方程右边的-2没有乘3,因而求得方程的解为x=3.试求a的值,并正确地解出方程.
,去分母时,方程右边的-2没有乘3,因而求得方程的解为x=3.试求a的值,并正确地解出方程. -
科目: 来源: 题型:
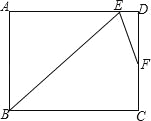
查看答案和解析>>【题目】(2016广西省贺州市第18题)在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,拉一条直的参照线,然后沿着线砌墙,其运用到的数学原理是( )
A. 两点确定一条直线 B. 过一点有无数条直线
C. 两点之间,线段最短 D. 连接两点之间的线段叫做两点之间的距离
相关试题

