【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

参考答案:
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】分析:(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;
(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;
(3)求出∠CDB=90°,再根据正方形的判定推出即可.
详解:(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴平行四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是:
∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E.

(1)求证:AC平分∠DAB;
(2)若∠B=60°,CD=2 ,求AE的长.
,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某次知识竞赛共有20道题,每一题答对得5分,答错或不答都扣3分.
(1)小明考了68分,那么小明答对了多少问题?
(2)小亮获得二等奖(70分~90分),请你算算小亮答对了几道题? -
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A,B,C表示的数分别是-6,10,12.点A以每秒3个单位长度的速度向右运动,同时线段BC以每秒1个单位长度的速度也向右运动.
(1)运动前线段AB的长度为________;
(2)当运动时间为多长时,点A和线段BC的中点重合?
(3)试探究是否存在运动到某一时刻,线段AB=
 AC?若存在,求出所有符合条件的点A表示的数;若不存在,请说明理由.
AC?若存在,求出所有符合条件的点A表示的数;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为加快城市群的建设与发展,在A,B两城市间新建一条城际铁路,建成后,铁路运行里程由现在的120km缩短至114km,城际铁路的设计平均时速要比现行的平均时速快110km,运行时间仅是现行时间的
 ,求建成后的城际铁路在A,B两地的运行时间.
,求建成后的城际铁路在A,B两地的运行时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列每组中的两个代数式,属于同类项的是( )
A.
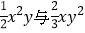 B.
B. 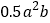 与
与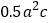 C.
C. 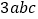 与
与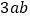 D.
D. 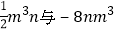
-
科目: 来源: 题型:
查看答案和解析>>【题目】省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动,某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如图两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题.

(1)m=%,这次共抽取名学生进行调查;并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多?
(3)如果该校共有1500名学生,请你估计该校骑自行车上学的学生有多少名?
相关试题

