【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系 ![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;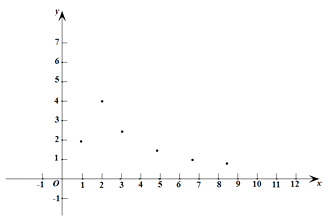
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为;
②该函数的一条性质: .
参考答案:
【答案】
(1)解:如下图:
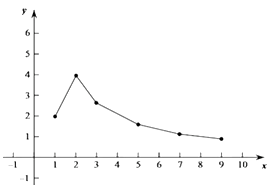
(2)(2.1到1.8之间都正确),该函数有最大值(其他正确性质都可以)
【解析】根据图像上的点顺次画出函数图象;根据画出的函数图象,得到x=4对应的函数值y在2.1到1.8之间都正确;该函数的一条性质是该函数有最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球队12名队员的年龄如下表所示:
年龄(岁)
18
19
20
21
人数
5
4
1
2
则这12名队员年龄的众数和中位数分别是( )
A.18,19B.18,19.5C.5,4D.5, 4.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(2a+b,b)与P1(8,﹣2)关于y轴对称,则a+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法.如图2,火柴盒的一个侧面ABCD倒下到AEFG的位置,连结CF,AB=a,BC=b,AC=c.

(1)请你结合图1用文字和符号语言分别叙述勾股定理;
(2)请利用直角梯形BCFG的面积证明勾股定理: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,点
中,点 是边
是边 的中点,连接
的中点,连接 并延长,交
并延长,交 延长线于点
延长线于点 连接
连接 .
.
(1)求证:四边形
 是平行四边形;
是平行四边形; (2)若
 ,则当
,则当
 时,四边形
时,四边形 是矩形.
是矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某水电站兴建了一个最大蓄水容量为12万米3的蓄水池,并配有2个流量相同的进水口和1个出水口.某天从0时至12时,进行机组试运行.其中,0时至2时打开2个进水口进水;2时,关闭1个进水口减缓进水速度,至蓄水池中水量达到最大蓄水容量后,随即关闭另一个进水口,并打开出水口,直至12时蓄水池中的水放完为止.
若这3个水口的水流都是匀速的,且2个进水口的水流速度一样,水池中的蓄水量 y(万米3)与时间t(时)之间的关系如图所示,请根据图象解决下列问题: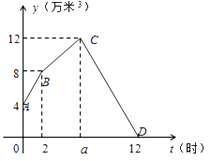
(1)蓄水池中原有蓄水万米3 , 蓄水池达最大蓄水量12万米3的时间a的值为;
(2)求线段BC、CD所表示的y与t之间的函数关系式;
(3)蓄水池中蓄水量维持在m万米3以上(含m万米3)的时间有3小时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图① ,菱形
 中,
中,
 ,动点
,动点 从点
从点 出发,沿折线
出发,沿折线 运动到点
运动到点 停止,动点
停止,动点 从点
从点 出发,沿线段
出发,沿线段 运动到点
运动到点 停止,它们运动的速度相同.设点
停止,它们运动的速度相同.设点 出发
出发 时,
时, 的面积为
的面积为
 .已知
.已知 与
与 之间的函数关系.如图 ②所示,其中
之间的函数关系.如图 ②所示,其中 为线段,曲线
为线段,曲线 为抛物线的一部分,请根据图中的信息,解答下列问题:
为抛物线的一部分,请根据图中的信息,解答下列问题:(1)当
 时,
时, 的面积 (填“变”或“不变”);
的面积 (填“变”或“不变”);(2)分别求出线段
 ,曲线
,曲线 所对应的函数表达式;
所对应的函数表达式;(3)当
 为何值时,
为何值时, 的面积是
的面积是
 ?
?

相关试题

