【题目】如图① ,菱形![]() 中,
中,![]()
![]() ,动点
,动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 运动到点
运动到点![]() 停止,动点
停止,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 运动到点
运动到点![]() 停止,它们运动的速度相同.设点
停止,它们运动的速度相同.设点![]() 出发
出发![]() 时,
时,![]() 的面积为
的面积为![]()
![]() .已知
.已知![]() 与
与![]() 之间的函数关系.如图 ②所示,其中
之间的函数关系.如图 ②所示,其中![]() 为线段,曲线
为线段,曲线![]() 为抛物线的一部分,请根据图中的信息,解答下列问题:
为抛物线的一部分,请根据图中的信息,解答下列问题:
(1)当![]() 时,
时,![]() 的面积 (填“变”或“不变”);
的面积 (填“变”或“不变”);
(2)分别求出线段![]() ,曲线
,曲线![]() 所对应的函数表达式;
所对应的函数表达式;
(3)当![]() 为何值时,
为何值时,![]() 的面积是
的面积是![]()
![]() ?
?


参考答案:
【答案】(1)不变;(2)y=10x;y=10(x-3)2;(3)当x=![]() 或3-
或3-![]() 时,△BPQ的面积是5cm2.
时,△BPQ的面积是5cm2.
【解析】
试题分析:(1)根据函数图象即可得到结论;
(2)设线段OM的函数表达式为y=kx,把(1,10)即可得到线段OM的函数表达式为y=10x;设曲线NK所对应的函数表达式y=a(x-3)2,把(2,10)代入得根据得到曲线NK所对应的函数表达式y=10(x-3)2;
(3)把y=5代入y=10x或y=10(x-3)2即可得到结论.
试题解析:(1)由函数图象知,当1<x<2时,△BPQ的面积始终等于10,
∴当1<x<2时,△BPQ的面积不变;
(2)设线段OM的函数表达式为y=kx,
把(1,10)代入得,k=10,
∴线段OM的函数表达式为y=10x;
设曲线NK所对应的函数表达式y=a(x-3)2,
把(2,10)代入得,10=a(2-3)2,
∴a=10,
∴曲线NK所对应的函数表达式y=10(x-3)2;
(3)把y=5代入y=10x得,x=![]() ,
,
把y=5代入y=10(x-3)2得,5=10(x-3)2,
∴x=3±![]() ,
,
∵3+![]() >3,
>3,
∴x=3-![]() ,
,
∴当x=![]() 或3-
或3-![]() 时,△BPQ的面积是5cm2.
时,△BPQ的面积是5cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x
···
1
2
3
5
7
9
···
y
···
1.98
3.95
2.63
1.58
1.13
0.88
···
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;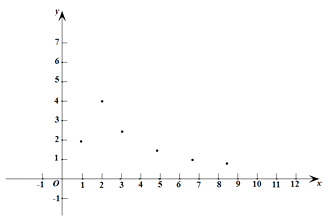
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为;
②该函数的一条性质: . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,点
中,点 是边
是边 的中点,连接
的中点,连接 并延长,交
并延长,交 延长线于点
延长线于点 连接
连接 .
.
(1)求证:四边形
 是平行四边形;
是平行四边形; (2)若
 ,则当
,则当
 时,四边形
时,四边形 是矩形.
是矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某水电站兴建了一个最大蓄水容量为12万米3的蓄水池,并配有2个流量相同的进水口和1个出水口.某天从0时至12时,进行机组试运行.其中,0时至2时打开2个进水口进水;2时,关闭1个进水口减缓进水速度,至蓄水池中水量达到最大蓄水容量后,随即关闭另一个进水口,并打开出水口,直至12时蓄水池中的水放完为止.
若这3个水口的水流都是匀速的,且2个进水口的水流速度一样,水池中的蓄水量 y(万米3)与时间t(时)之间的关系如图所示,请根据图象解决下列问题: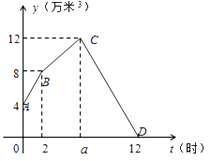
(1)蓄水池中原有蓄水万米3 , 蓄水池达最大蓄水量12万米3的时间a的值为;
(2)求线段BC、CD所表示的y与t之间的函数关系式;
(3)蓄水池中蓄水量维持在m万米3以上(含m万米3)的时间有3小时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(友情提醒:正方形的四条边都相等,即AB=BC=CD=DA;四个内角都是90°,即∠A=∠B=∠C=∠D=90°)
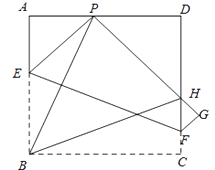
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,求出BE的长.(用含x的代数式表式) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
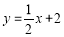 与x轴交于点A,与y轴交于点C,抛物线
与x轴交于点A,与y轴交于点C,抛物线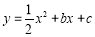 经过A、C两点,与x轴的另一交点为点B.
经过A、C两点,与x轴的另一交点为点B.(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点;
①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为
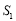 ,△BCE的面积为
,△BCE的面积为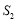 ,求
,求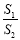 的最大值;
的最大值;②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=
 ACBD,其中正确的结论有( )
ACBD,其中正确的结论有( )
A.①②
B.①③
C.②③
D.①③②
相关试题

