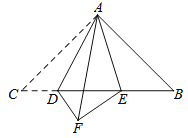
【题目】已知:如图,△ABC 中,∠CAB=90°,AC=AB,点 D、E 是 BC 上的两点,且∠DAE=45°,△ADC 与△ADF 关于直线AD 对称.
(1)求证:△AEF≌△AEB;
(2)求∠DFE 的度数.
参考答案:
【答案】(1)详见解析;(2)90°.
【解析】
(1)根据折叠的性质得到△ADF≌△ADC,根据全等三角形的性质得到AC=AF,CD=FD,∠C=∠DFA,∠CAD=∠FAD,由于AB=AC,于是得到AF=AB,证得∠FAE=∠BAE,即可得到结论;
(2)由(1)知△AFE≌△ABE,根据全等三角形的性质得到∠AFE=∠B,即可得到结论.
(1)∵把△ADC沿着AD折叠,得到△ADF,∴△ADF≌△ADC;
∴AC=AF,CD=FD,∠C=∠DFA,∠CAD=∠FAD.
∵AB=AC,∴AF=AB.
∵∠DAE=45°,∴∠CAD+∠BAE=45°.
∵∠CAD=∠FAD,∴∠FAE=∠BAE.
在△AFE与△ABE中,∵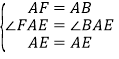 ,∴△AEF≌△AEB;
,∴△AEF≌△AEB;
(2)由(1)知△AEF≌△AEB,∴∠AFE=∠B.
∵∠C=∠DFA,∴∠DFE=∠DFA+∠EFA=∠B+∠C=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=45°,点P在∠AOB的内部.P′与P关于OA对称,P"与P关于OB对称,则O、P′、P"三点所构成的三角形是( )

A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.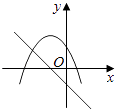
B.
C.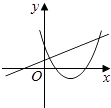
D.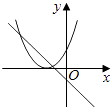
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a≠0)的图象与反比例函数y=
 (k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.
(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.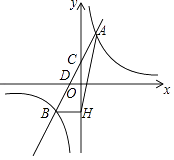
(1)求一次函数和反比例函数的解析式;
(2)求△ABH面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图 1,在四边形 ABCD 中,AB∥DC,E 是 BC 中点,若 AE 是∠BAD 的平分线,试探究 AB,AD,DC 之间的数量关系,请直接写出结论,无需证明.
(2)如图 2,在四边形ABCD 中,AB∥DC,AF 与DC 的延长线交于点F,E 是BC 中点,若AE 是∠BAF 的平分线,试探究AB,AF,CF 之间的数量关系,证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )

A.10 海里
海里
B.10 海里
海里
C.10 海里
海里
D.20 海里
海里 -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=1,AD=
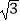 ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED,正确的个数是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED,正确的个数是( ) 
A.1
B.2
C.3
D.4
相关试题

