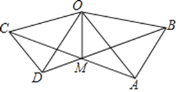
【题目】如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的是____________________________
参考答案:
【答案】①②④
【解析】
由SAS证明△AOC≌△BOD得出∠OCA=∠ODB,AC=BD,①正确;
由全等三角形的性质得出∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,得出∠AMB=∠AOB=40°,②正确;
作OG⊥MC于G,OH⊥MB于H,如图2所示:则∠OGC=∠OHD=90°,由AAS证明△OCG≌△ODH(AAS),得出OG=OH,由角平分线的判定方法得出MO平分∠BMC,④正确;
由∠AOB=∠COD,得出当∠DOM=∠AOM时,OM才平分∠BOC,假设∠DOM=∠AOM,由△AOC≌△BOD得出∠COM=∠BOM,由MO平分∠BMC得出∠CMO=∠BMO,推出△COM≌△BOM,得OB=OC,而OA=OB,所以OA=OC,而OA>OC,故③错误;即可得出结论.
解:∵∠AOB=∠COD=40°,
∴∠AOB+∠AOD=∠COD+∠AOD,
即∠AOC=∠BOD,
在△AOC和△BOD中,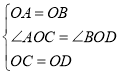
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,AC=BD,①正确;
∴∠OAC=∠OBD,
由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,
∴∠AMB=∠AOB=40°,②正确;
作OG⊥MC于G,OH⊥MB于H,如图2所示:

则∠OGC=∠OHD=90°,
在△OCG和△ODH中,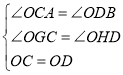
∴△OCG≌△ODH(AAS),
∴OG=OH,
∴MO平分∠BMC,④正确;
∵∠AOB=∠COD,
∴当∠DOM=∠AOM时,OM才平分∠BOC,
假设∠DOM=∠AOM
∵△AOC≌△BOD,
∴∠COM=∠BOM,
∵MO平分∠BMC,
∴∠CMO=∠BMO,
在△COM和△BOM中,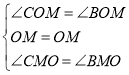
∴△COM≌△BOM(ASA),
∴OB=OC,
∵OA=OB
∴OA=OC
与OA>OC矛盾,
∴③错误;
正确的是①②④;
故答案为:①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个四位自然数的百位数字大于或等于十位数字,且千位数字等于百位数字与十位数字的和,个位数字等于百位与十位数字的差,则我们称这个四位数为亲密数,例如:自然数4312,其中3>1,4=3+1,2=3-1,所以4312是亲密数;
(1)最小的亲密数是 ,最大的亲密数是 ;
(2)若把一个亲密数的千位数字与个位数字交换,得到的新数叫做这个亲密数的友谊数,请证明任意一个亲密数和它的友谊数的差都能被原亲密数的十位数字整除;
(3)若一个亲密数的后三位数字所表示的数与千位数字所表示的数的7倍之差能被13整除,请求出这个亲密数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B>90°,CD为∠ACB的角平分线,在AC边上取点E,使DE=DB,且∠AED>90°.若∠A=α,∠ACB=β,则( )

A.∠AED=180°﹣α﹣βB.∠AED=180°﹣α﹣
 β
βC.∠AED=90°﹣α+βD.∠AED=90°+α+
 β
β -
科目: 来源: 题型:
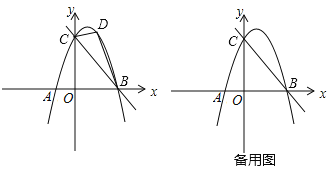
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与
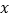 轴相交于A、B两点,与
轴相交于A、B两点,与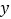 轴相交于点C,OA=1,OC=3,连接BC.
轴相交于点C,OA=1,OC=3,连接BC.(1)求b的值;
(2)点D是直线BC上方抛物线一动点(点B、C除外),当△BCD的面积取得最大值时,在
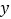 轴上是否存在一点P,使得|PB﹣PD|最大,若存在,请求出点P的坐标;若不存在,请说明理由.
轴上是否存在一点P,使得|PB﹣PD|最大,若存在,请求出点P的坐标;若不存在,请说明理由.(3)在(2)的条件下,若在平面上存在点Q,使得以点B、C、D、Q为顶点的四边形为平行四边形,请直接写出点Q坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
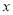 、
、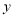 的方程组
的方程组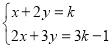 以下结论:①当
以下结论:①当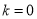 时,方程组的解也是方程
时,方程组的解也是方程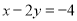 的解;②存在实数
的解;②存在实数 ,使得
,使得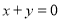 ;③当
;③当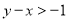 时,
时,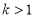 ;④不论
;④不论 取什么实数,
取什么实数,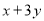 的值始终不变,其中正确的是( )
的值始终不变,其中正确的是( )A.①②③B.①②④C.①③④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出五个等量关系:①AD=BC;②AC=BD;③CE=DE;④∠D=∠C;⑤∠DAB=∠CBA.

请你以其中两个为条件,另外三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.
已知:
求证:
证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列有四个结论:①若
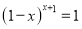 ,则
,则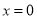 ;
;②若
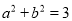 ,
,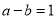 ,则
,则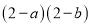 的值为
的值为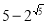 ;
;③若
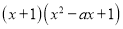 的运算结果中不含
的运算结果中不含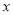 项,则
项,则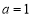 ;
;④若
 ,
,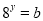 ,则
,则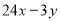 可表示为
可表示为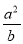 .
.其中正确的是(填序号)是:______.
相关试题

