【题目】如果一个四位自然数的百位数字大于或等于十位数字,且千位数字等于百位数字与十位数字的和,个位数字等于百位与十位数字的差,则我们称这个四位数为亲密数,例如:自然数4312,其中3>1,4=3+1,2=3-1,所以4312是亲密数;
(1)最小的亲密数是 ,最大的亲密数是 ;
(2)若把一个亲密数的千位数字与个位数字交换,得到的新数叫做这个亲密数的友谊数,请证明任意一个亲密数和它的友谊数的差都能被原亲密数的十位数字整除;
(3)若一个亲密数的后三位数字所表示的数与千位数字所表示的数的7倍之差能被13整除,请求出这个亲密数.
参考答案:
【答案】(1)1101,9909;(2)证明见解析;(3)亲密数为5321或9817.
【解析】
(1)设亲密数为![]() ,求最小的亲密数时,先确定a=1,再根据a=b+c,d=b﹣c确定b、c、d的值,从而可得最小的亲密数;求最大的亲密数时,先确定a=9,同理可得最大的亲密数;
,求最小的亲密数时,先确定a=1,再根据a=b+c,d=b﹣c确定b、c、d的值,从而可得最小的亲密数;求最大的亲密数时,先确定a=9,同理可得最大的亲密数;
(2)分别表示亲密数和友谊数:亲密数:![]() =1000a+100b+10c+d,友谊数:
=1000a+100b+10c+d,友谊数:![]() =1000d+100b+10c+a,相减后可得结论;
=1000d+100b+10c+a,相减后可得结论;
(3)根据题意表示![]() ﹣7a=100b+10c+d﹣7a,化为关于b和c的代数式,根据b是1至9的自然数对:94b+2c进行分析,
﹣7a=100b+10c+d﹣7a,化为关于b和c的代数式,根据b是1至9的自然数对:94b+2c进行分析,![]() =7b+
=7b+![]() 为整数,即3b+2c为13的倍数,分情况讨论3b+2c的值可得结论.
为整数,即3b+2c为13的倍数,分情况讨论3b+2c的值可得结论.
设亲密数为![]() ,且b≥c,a=b+c,d=b-c,a、b、c、d都是自然数,
,且b≥c,a=b+c,d=b-c,a、b、c、d都是自然数,
(1)当a为最小时,则a=1,
∴b+c=a=1,
∵b≥c,
∴b=1,c=0,
∴d=b-c=1-0=1,
∴最小的亲密数是1101,
当a最大时,即a=9,
∴b+c=a=9,
∵b≥c,
当![]() 最大时,即b最大为9,
最大时,即b最大为9,
∴c=0,
∴d=b-c=9-0=9,
∴最大的亲密数是9909,
故答案为:1101,9909;
(2)证明:亲密数:![]() =1000a+100b+10c+d①,
=1000a+100b+10c+d①,
友谊数:![]() =1000d+100b+10c+a②,
=1000d+100b+10c+a②,
∵a=b+c,d=b-c,
∴a-d=(b+c)-(b-c)=2c>0,
∴a>d,a=2c+d,
①-②得:999a-999d=999(a-d)=999(2c+d-d)=1998c,
∵原亲密数的十位数字为c,
∴任意一个亲密数和它的友谊数的差都能被原亲密数的十位数字整除;
(3)![]() =100b+10c+d,
=100b+10c+d,
∵a=b+c,d=b-c,
∴![]() -7a=100b+10c+d-7a=100b+10c+b-c-7(b+c)=94b+2c,
-7a=100b+10c+d-7a=100b+10c+b-c-7(b+c)=94b+2c,
由题意得:![]() 为整数,
为整数,
即3b+2c为13的倍数,
∵0≤b≤9,0≤c≤9,b、c为整数,且1≤b+c≤9,
∴2≤3b+2c≤27,
∴3b+2c=13或26,
①当3b+2c=13时(b≥c),
得![]() ,
,
∴亲密数为5321;
②若3b+2c=26(b≥c),
则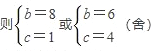 ,
,
∴亲密数为9817,
综上所述,亲密数为5321或9817.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数
 的图象交于第二、四象限内的A,B两点,与
的图象交于第二、四象限内的A,B两点,与 轴交于C点,过点A作AH⊥
轴交于C点,过点A作AH⊥ 轴,垂足为H,OH=3,tan∠AOH=
轴,垂足为H,OH=3,tan∠AOH= ,点B的坐标为(
,点B的坐标为( ,﹣2).
,﹣2).(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个等腰Rt△ABC,Rt△CEF有公共顶点C,∠ABC﹣∠CEF=90°,连接AF,M是AF的中点
(1)如图1,当CB与CE在同一直线上时,连接CM,若CB=1,CE=2,求CM的长.
(2)如图2,连接MB,ME,当∠BCE=45°时,求证:BM=ME.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B>90°,CD为∠ACB的角平分线,在AC边上取点E,使DE=DB,且∠AED>90°.若∠A=α,∠ACB=β,则( )

A.∠AED=180°﹣α﹣βB.∠AED=180°﹣α﹣
 β
βC.∠AED=90°﹣α+βD.∠AED=90°+α+
 β
β -
科目: 来源: 题型:
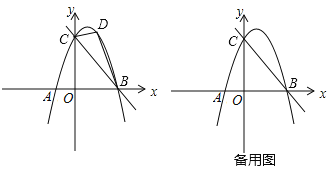
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与
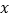 轴相交于A、B两点,与
轴相交于A、B两点,与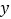 轴相交于点C,OA=1,OC=3,连接BC.
轴相交于点C,OA=1,OC=3,连接BC.(1)求b的值;
(2)点D是直线BC上方抛物线一动点(点B、C除外),当△BCD的面积取得最大值时,在
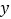 轴上是否存在一点P,使得|PB﹣PD|最大,若存在,请求出点P的坐标;若不存在,请说明理由.
轴上是否存在一点P,使得|PB﹣PD|最大,若存在,请求出点P的坐标;若不存在,请说明理由.(3)在(2)的条件下,若在平面上存在点Q,使得以点B、C、D、Q为顶点的四边形为平行四边形,请直接写出点Q坐标.
-
科目: 来源: 题型:
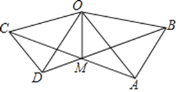
查看答案和解析>>【题目】如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的是____________________________
相关试题

