【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点,作BM⊥AE于点M,作KN⊥AE于点N,连结MO、NO,以下四个结论:①△OMN是等腰三角形;②tan∠OMN= ![]() ;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )
;③BP=4PK;④PMPA=3PD2 , 其中正确的是( )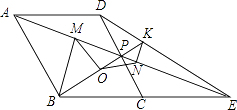
A.①②③
B.①②④
C.①③④
D.②③④
参考答案:
【答案】B
【解析】解:作PI∥CE交DE于I,
∵四边形ABCD为菱形,
∴AD∥BC,
∴∠DAP=∠CEP,∠ADP=∠ECP,
在△ADP和△ECP中,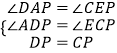 ,
,
∴△ADP≌△ECP,
∴AD=CE,
则 ![]() ,又点P是CD的中点,
,又点P是CD的中点,
∴ ![]() =
= ![]() ,
,
∵AD=CE,
∴ ![]() =
= ![]() ,
,
∴BP=3PK,
故③错误;
作OG⊥AE于G,
∵BM丄AE于M,KN丄AE于N,
∴BM∥OG∥KN,
∵点O是线段BK的中点,
∴MG=NG,又OG⊥MN,
∴OM=ON,
即△MON是等腰三角形,故①正确;
由题意得,△BPC,△AMB,△ABP为直角三角形,
设BC=2,则CP=1,由勾股定理得,BP= ![]() ,
,
则AP= ![]() ,
,
根据三角形面积公式,BM= ![]() ,
,
∵点O是线段BK的中点,
∴PB=3PO,
∴OG= ![]() BM=
BM= ![]() ,
,
MG= ![]() MP=
MP= ![]() ,
,
tan∠OMN= ![]() =
= ![]() ,故②正确;
,故②正确;
∵∠ABP=90°,BM⊥AP,
∴PB2=PMPA,
∵∠BCD=60°,
∴∠ABC=120°,
∴∠PBC=30°,
∴∠BPC=90°,
∴PB= ![]() PC,
PC,
∵PD=PC,
∴PB2=3PD,
∴PMPA=3PD2 , 故④正确.
故选B.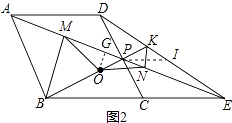
根据菱形的性质得到AD∥BC,根据平行线的性质得到对应角相等,根据全等三角形的判定定理△ADP≌△ECP,由相似三角形的性质得到AD=CE,作PI∥CE交DE于I,根据点P是CD的中点证明CE=2PI,BE=4PI,根据相似三角形的性质得到 ![]() =
= ![]() ,得到BP=3PK,故③错误;作OG⊥AE于G,根据平行线等分线段定理得到MG=NG,又OG⊥MN,证明△MON是等腰三角形,故①正确;根据直角三角形的性质和锐角三角函数求出∠OMN=
,得到BP=3PK,故③错误;作OG⊥AE于G,根据平行线等分线段定理得到MG=NG,又OG⊥MN,证明△MON是等腰三角形,故①正确;根据直角三角形的性质和锐角三角函数求出∠OMN= ![]() ,故②正确;然后根据射影定理和三角函数即可得到PMPA=3PD2 , 故④正确.
,故②正确;然后根据射影定理和三角函数即可得到PMPA=3PD2 , 故④正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )

A.∠ABP=∠C
B.∠APB=∠ABC
C.AB2=AP?AC
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )
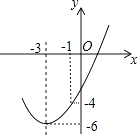
A.b2>4ac
B.ax2+bx+c≥﹣6
C.若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对全校学生60秒跳绳的次数进行了统计,全校学生60秒跳绳的平均次数是100次,某班体育委员统计了全班50名学生60秒跳绳的成绩,列出的频数分布直方图如图所示(每个分组包括左端点,不包括右端点).
(1)该班学生60秒跳绳的平均次数至少是多少?是否超过全校平均次数?
(2)该班一个学生说:“我的跳绳成绩在我班是中位数.”请你给出该生跳绳成绩所在的范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)在上学期的几次测试中,小张和小王的几次数学成绩(单位:分)如下表:

两人都说自己的数学成绩更好.请你想一想:
(1)小张可能是根据什么来判断的?小王可能是根据什么来判断的?
(2)你能根据小张的想法设计一种方案使小张的成绩比小王的高吗?写出你的方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算。
(1)计算: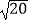 +(﹣3)2﹣(
+(﹣3)2﹣( 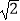 ﹣1)0 .
﹣1)0 .
(2)化简:(2+m)(2﹣m)+m(m﹣1). -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,后求值:
(1)
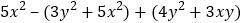 ,其中
,其中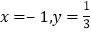 ;
;(2)
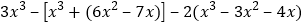 ,其中
,其中 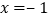 ;
;(3)
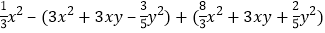 ,其中
,其中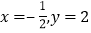 .
.
相关试题

