【题目】(1)操作发现:
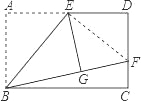
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.

(2)问题解决:
保持(1)中的条件不变,若DC=2DF,求![]() 的值;
的值;
(3)类比探求:
保持(1)中条件不变,若DC=nDF,求![]() 的值.
的值.
参考答案:
【答案】(1)同意,理由见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)求简单的线段相等,可证线段所在的三角形全等,即连接EF,证△EGF≌△EDF即可;
(2)可设DF=x,BC=y;进而可用x表示出DC、AB的长,根据折叠的性质知AB=BG,即可得到BG的表达式,由(1)证得GF=DF,那么GF=x,由此可求出BF的表达式,进而可在Rt△BFC中,根据勾股定理求出x、y的比例关系,即可得到![]() 的值;
的值;
(3)方法同(2).
试题解析:(1)同意,连接EF,
则根据翻折不变性得,
∠EGF=∠D=90°,EG=AE=ED,EF=EF,
在Rt△EGF和Rt△EDF中,
![]()
∴Rt△EGF≌Rt△EDF(HL),
∴GF=DF;
(2)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=2DF,
∴CF=x,DC=AB=BG=2x,
∴BF=BG+GF=3x;
在Rt△BCF中,BC2+CF2=BF2,即y2+x2=(3x)2
∴y=2![]() x,
x,
∴![]() ;
;
(3)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=nDF,
∴BF=BG+GF=(n+1)x
在Rt△BCF中,BC2+CF2=BF2,即y2+[(n-1)x]2=[(n+1)x]2
∴y=2x![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用同一种规格的下列多边形瓷砖不能镶嵌成平面图案的是( )
A.三角形B.正方形C.正五边形D.正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,A(a,0),C(b,2),过C作CB⊥x轴,且满足(a+b)2+
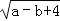 =0.
=0.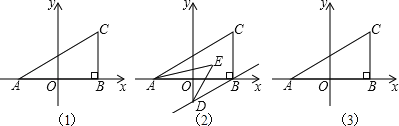
(1)求三角形ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:

(2) 解方程组

(3)解方程组

(4)如果关于x,y的方程组
 的解满足3x+y=5,求k的值
的解满足3x+y=5,求k的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】现有一些分别标有-1,2,-4,8,-16,32,…的卡片,这些卡片上的数字是按一定规律排列的,小明拿到了相邻的三张卡片,且卡片上的数字之和为96,则小明拿到的三张卡片上分别标有什么数字?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两站相距336千米,一列慢车从甲站开出,每小时行驶72千米,一列快车从乙站开出,每小时行驶96千米.
(1)若两车同时相向而行,则几小时后相遇?几小时后相距84千米?
(2)若两车同时反向而行,则几小时后相距672千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明随机写了一串数字“1,2,3,3,2,1,1,1,2,2,3,3,”,则数字3出现的频数( )
A.6B.5C.4D.3
相关试题

