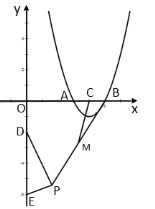
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,对称轴与
两点,对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 是平面内一动点,且满足
是平面内一动点,且满足![]() ,
,![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .则线段
.则线段![]() 的最大值是( ).
的最大值是( ).
A.3B.![]() C.
C.![]() D.5
D.5
参考答案:
【答案】C
【解析】
解方程x28x+15=0得A(3,0),利用抛物线的性质得到C点为AB的中点,再根据圆周角定理得到点P在以DE为直径的圆上,圆心Q点的坐标为(4,0),接着计算出AQ=5,⊙Q的半径为2,延长AQ交⊙Q于F,此时AF的最大值为7,连接AP,利用三角形的中位线性质得到CM=![]() AP,从而得到CM的最大值.
AP,从而得到CM的最大值.
解方程x28x+15=0得x1=3,x2=5,则A(3,0),
∵抛物线的对称轴与x轴交于点C,
∴C点为AB的中点,
∵∠DPE=90°,
∴点P在以DE为直径的圆上,圆心Q点的坐标为(4,0),
AQ=![]() =5,⊙Q的半径为2,
=5,⊙Q的半径为2,
延长AQ交⊙Q于F,此时AF最大,最大值为2+5=7,
连接AP,
∵M是线段PB的中点,
∴CM为△ABP为中位线,
∴CM=![]() AP,
AP,
∴CM的最大值为![]() .
.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
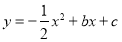 过点
过点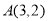 ,且与直线
,且与直线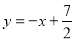 交于B、C两点,点B的坐标为
交于B、C两点,点B的坐标为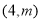 .
.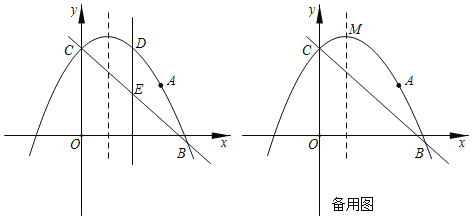
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线
 上方的一点,过点D作
上方的一点,过点D作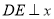 轴交直线
轴交直线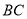 于点E,点P为对称轴上一动点,当线段
于点E,点P为对称轴上一动点,当线段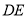 的长度最大时,求
的长度最大时,求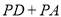 的最小值;
的最小值;(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使
 ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年是我国建国70周年,回顾过去展望未来,创新是引领发展的第一动力,北京科技创新能力不断增强,下面的统计图反映了2010﹣2018年北京市每万人发明专利申请数与授权数的情况.
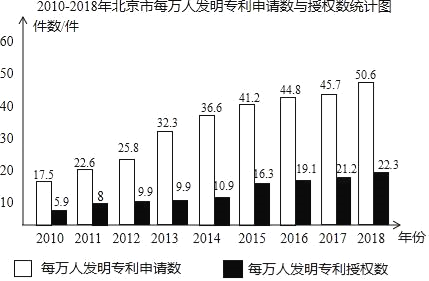
根据统计图提供的信息,下列推断合理的是( )
A. 2010﹣2018年,北京市毎万人发明专利授权数逐年增长
B. 2010﹣2018年,北京市毎万人发明专利授权数的平均数超过10件
C. 2010年申请后得到授权的比例最低
D. 2018年申请后得到授权的比例最高
-
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧原长(不挂重物)15cm,弹簧总长L(cm)与重物质量x(kg)的关系如下表所示:
弹簧总长L(cm)
16
17
18
19
20
重物重量x(kg)
0.5
1.0
1.5
2.0
2.5
当重物质量为5kg(在弹性限度内)时,弹簧总长L(cm)是( )
A.22.5B.25C.27.5D.30
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C是⊙O上的三个点,点D在BC的延长线上.有如下四个结论:①在∠ABC所对的弧上存在一点E,使得∠BCE=∠DCE;②在∠ABC所对的弧上存在一点E,使得∠BAE=∠AEC;③在∠ABC所对的弧上存在一点E,使得EO平分∠AEC;④在∠ABC所对的弧上任意取一点E(不与点A,C重合) ,∠DCE=∠ABO +∠AEO均成立.上述结论中,所有正确结论的序号是( )

A. ①②③ B. ①③④ C. ②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系
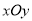 中的点
中的点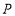 ,
,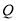 ,给出如下定义:若
,给出如下定义:若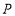 ,
,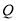 为某个三角形的顶点,且边
为某个三角形的顶点,且边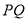 上的高
上的高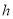 ,满足
,满足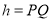 ,则称该三角形为点
,则称该三角形为点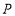 ,
,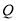 的“生成三角形”.
的“生成三角形”.(1)已知点
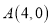 ;
;①若以线段
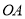 为底的某等腰三角形恰好是点
为底的某等腰三角形恰好是点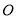 ,
,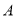 的“生成三角形”,求该三角形的腰长;
的“生成三角形”,求该三角形的腰长;②若
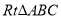 是点
是点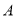 ,
,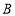 的“生成三角形”,且点
的“生成三角形”,且点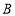 在
在 轴上,点
轴上,点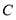 在直线
在直线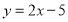 上,则点
上,则点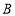 的坐标为______;
的坐标为______;(2)
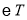 的圆心为点
的圆心为点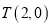 ,半径为2,点
,半径为2,点 的坐标为
的坐标为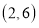 ,
,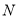 为直线
为直线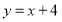 上一点,若存在
上一点,若存在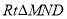 ,是点
,是点 ,
,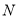 的“生成三角形”,且边
的“生成三角形”,且边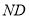 与
与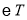 有公共点,直接写出点
有公共点,直接写出点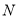 的横坐标
的横坐标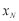 的取值范围.
的取值范围.
相关试题

