【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,
,![]() ,给出如下定义:若
,给出如下定义:若![]() ,
,![]() 为某个三角形的顶点,且边
为某个三角形的顶点,且边![]() 上的高
上的高![]() ,满足
,满足![]() ,则称该三角形为点
,则称该三角形为点![]() ,
,![]() 的“生成三角形”.
的“生成三角形”.
(1)已知点![]() ;
;
①若以线段![]() 为底的某等腰三角形恰好是点
为底的某等腰三角形恰好是点![]() ,
,![]() 的“生成三角形”,求该三角形的腰长;
的“生成三角形”,求该三角形的腰长;
②若![]() 是点
是点![]() ,
,![]() 的“生成三角形”,且点
的“生成三角形”,且点![]() 在
在![]() 轴上,点
轴上,点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的坐标为______;
的坐标为______;
(2)![]() 的圆心为点
的圆心为点![]() ,半径为2,点
,半径为2,点![]() 的坐标为
的坐标为![]() ,
,![]() 为直线
为直线![]() 上一点,若存在
上一点,若存在![]() ,是点
,是点![]() ,
,![]() 的“生成三角形”,且边
的“生成三角形”,且边![]() 与
与![]() 有公共点,直接写出点
有公共点,直接写出点![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)①该三角形的腰长为![]() ;②
;②![]() ,
,![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)①画图,不妨设满足条件的三角形为等腰![]() ,则
,则![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,由勾股定理可求得其腰长;
,由勾股定理可求得其腰长;
②分点![]() 为直角顶点和点
为直角顶点和点![]() 为直角顶点两种情况,结合图形可得结论;
为直角顶点两种情况,结合图形可得结论;
(2)分点![]() 为直角顶点和点
为直角顶点和点![]() 为直角顶点,由图形可得答案.
为直角顶点,由图形可得答案.
(1)①如图,不妨设满足条件的三角形为等腰![]() ,则
,则![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,
,
∴![]() ,
,
∵以线段![]() 为底的等腰
为底的等腰![]() 恰好是点
恰好是点![]() ,
,![]() 的“生成三角形”,
的“生成三角形”,
∴![]() .
.
∴![]() ,
,
答:该三角形的腰长为![]() .
.

②如图所示:若![]() 为直角顶点时,点
为直角顶点时,点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
若![]() 为直角顶点时,点
为直角顶点时,点![]() 的坐标为
的坐标为![]() 或
或![]() ,
,
综上,点![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() .
.

(2)由图可得:
若![]() 为直角顶点:
为直角顶点:![]() ;
;

若![]() 为直角顶点:
为直角顶点:![]() ;
;

综上,![]() .
.
答:点![]() 的横坐标
的横坐标![]() 的取值范围为:
的取值范围为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
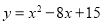 与
与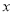 轴交于
轴交于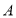 、
、 两点,对称轴与
两点,对称轴与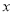 轴交于点
轴交于点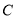 ,点
,点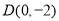 ,点
,点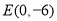 ,点
,点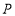 是平面内一动点,且满足
是平面内一动点,且满足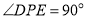 ,
,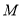 是线段
是线段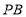 的中点,连结
的中点,连结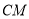 .则线段
.则线段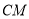 的最大值是( ).
的最大值是( ).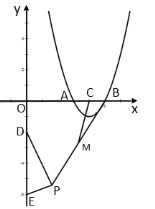
A.3B.
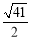 C.
C.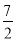 D.5
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C是⊙O上的三个点,点D在BC的延长线上.有如下四个结论:①在∠ABC所对的弧上存在一点E,使得∠BCE=∠DCE;②在∠ABC所对的弧上存在一点E,使得∠BAE=∠AEC;③在∠ABC所对的弧上存在一点E,使得EO平分∠AEC;④在∠ABC所对的弧上任意取一点E(不与点A,C重合) ,∠DCE=∠ABO +∠AEO均成立.上述结论中,所有正确结论的序号是( )

A. ①②③ B. ①③④ C. ②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
-
科目: 来源: 题型:
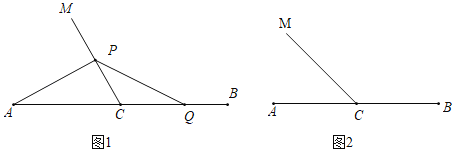
查看答案和解析>>【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣6mx+9m+1(m≠0).
(1)求抛物线的顶点坐标;
(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧),且AB=4,求m的值.
(3)已知四个点C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若抛物线与线段CD和线段EF都没有公共点,请直接写出m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆
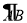 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1
位置2
位置3
位置4
位置5
位置6
位置…
AP
0.00
1.00
2.00
3.00
4.00
5.00
…
BC
6.00
5.48
4.90
4.24
3.46
2.45
…
OD
6.71
7.24
7.07
6.71
6.16
5.33
…
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.
相关试题

