【题目】如图,抛物线![]() 过点
过点![]() ,且与直线
,且与直线![]() 交于B、C两点,点B的坐标为
交于B、C两点,点B的坐标为![]() .
.
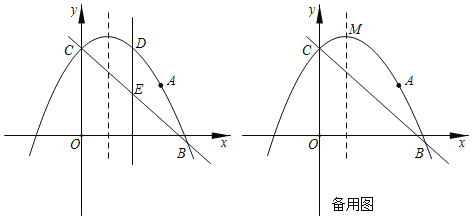
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线![]() 上方的一点,过点D作
上方的一点,过点D作![]() 轴交直线
轴交直线![]() 于点E,点P为对称轴上一动点,当线段
于点E,点P为对称轴上一动点,当线段![]() 的长度最大时,求
的长度最大时,求![]() 的最小值;
的最小值;
(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使![]() ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线的解析式![]() ;(2)
;(2)![]() 的最小值为
的最小值为![]() ;(3)点Q的坐标:
;(3)点Q的坐标:![]() 、
、![]() .
.
【解析】
(1)将点B的坐标为![]() 代入
代入![]() ,
,![]() ,B的坐标为
,B的坐标为![]() ,将
,将![]() ,
,![]() 代入
代入![]() ,解得
,解得![]() ,
,![]() ,因此抛物线的解析式
,因此抛物线的解析式![]() ;
;
(2)设![]() ,则
,则![]() ,
,![]() ,当
,当![]() 时,
时,![]() 有最大值为2,此时
有最大值为2,此时![]() ,作点A关于对称轴的对称点
,作点A关于对称轴的对称点![]() ,连接
,连接![]() ,与对称轴交于点P.
,与对称轴交于点P.![]() ,此时
,此时![]() 最小;
最小;
(3)作![]() 轴于点H,连接
轴于点H,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,由
,由![]() ,
,![]() ,可得
,可得![]() ,
,![]() 因为
因为![]() ,
,![]() ,所以
,所以![]() ,可知
,可知![]() 外接圆的圆心为H,于是
外接圆的圆心为H,于是![]() 设
设![]() ,则
,则![]() ,
,![]() 或
或![]() ,求得符合题意的点Q的坐标:
,求得符合题意的点Q的坐标:![]() 、
、![]() .
.
解:(1)将点B的坐标为![]() 代入
代入![]() ,
,
![]() ,
,
∴B的坐标为![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,
,
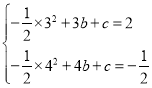
解得![]() ,
,![]() ,
,
∴抛物线的解析式![]() ;
;
(2)设![]() ,则
,则![]() ,
,
![]() ,
,
∴当![]() 时,
时,![]() 有最大值为2,
有最大值为2,
此时![]() ,
,
作点A关于对称轴的对称点![]() ,连接
,连接![]() ,与对称轴交于点P.
,与对称轴交于点P.

![]() ,此时
,此时![]() 最小,
最小,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
即![]() 的最小值为
的最小值为![]() ;
;
(3)作![]() 轴于点H,连接
轴于点H,连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,

∵抛物线的解析式![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]()
∵![]() ,
,
![]() ,
,
∴![]() ,
,
可知![]() 外接圆的圆心为H,
外接圆的圆心为H,
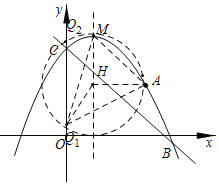
∴![]()
设![]() ,
,
则![]() ,
,
![]() 或
或![]()
∴符合题意的点Q的坐标:![]() 、
、![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进
 、
、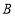 两种粽子1100个,购买
两种粽子1100个,购买 种粽子与购买
种粽子与购买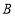 种粽子的费用相同,已知
种粽子的费用相同,已知 粽子的单价是
粽子的单价是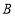 种粽子单价的1.2倍.
种粽子单价的1.2倍.(1)求
 、
、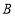 两种粽子的单价各是多少?
两种粽子的单价各是多少?(2)若计划用不超过7000元的资金再次购买
 、
、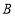 两种粽子共2600个,已知
两种粽子共2600个,已知 、
、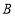 两种粽子的进价不变,求
两种粽子的进价不变,求 中粽子最多能购进多少个?
中粽子最多能购进多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有若干间标准房,当标准房的价格为
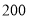 元时,每天入住的国间数为
元时,每天入住的国间数为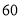 间,经市场调查表明,该宾馆每间标准房的价格在
间,经市场调查表明,该宾馆每间标准房的价格在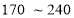 元之间(含
元之间(含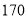 元,
元,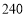 元)浮动时,每天人住的房间数
元)浮动时,每天人住的房间数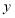 (间)与每间标准房的价格
(间)与每间标准房的价格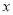 (元)的数据如下表:
(元)的数据如下表: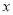 (元)
(元)……
190
200
210
220
……
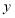 (元)
(元)……
65
60
55
50
……
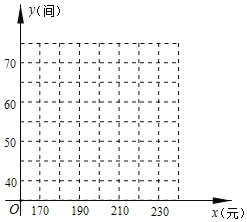
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)猜想(1)中的图象是什么函数的图象,求
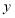 关于
关于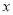 的函数表达式,并写出自变量
的函数表达式,并写出自变量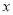 的取值范围.
的取值范围.(3)设客房的日营业额为W (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内,给定不在同一条直线上的点
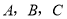 (如图所示),点
(如图所示),点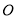 到点
到点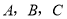 的距离均等于
的距离均等于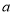 (
(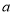 为常数),到点
为常数),到点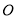 的距离等于
的距离等于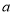 的所有点组成图形
的所有点组成图形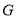 ,
,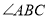 的平分线交图形
的平分线交图形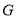 于点
于点 ,连接
,连接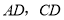 .
.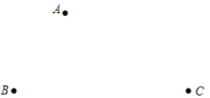
(1)求证:
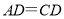 ;
;(2)过点
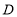 作
作 ,垂足为
,垂足为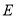 ,作
,作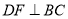 ,垂足为
,垂足为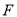 ,延长
,延长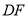 交图形
交图形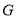 于点
于点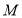 ,连接
,连接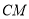 .若
.若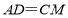 ,求直线
,求直线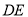 与图形
与图形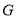 的公共点个数.
的公共点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明从如图所示的二次函数
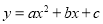 的图象中,观察得出了下面五条信息:①c>0,②abc<0,③a-b+c>0,④
的图象中,观察得出了下面五条信息:①c>0,②abc<0,③a-b+c>0,④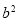 >4ac,⑤2a=-2b,其中正确结论是( ).
>4ac,⑤2a=-2b,其中正确结论是( ).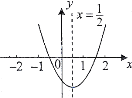
A.①②④B.②③④C.③④⑤D.①③⑤
-
科目: 来源: 题型:
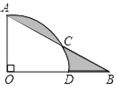
查看答案和解析>>【题目】如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点A、点C,交OB于点D,若OA=3,则阴影都分的面积为___________.
-
科目: 来源: 题型:
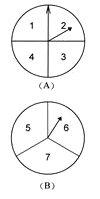
查看答案和解析>>【题目】甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜.
(1)用列表法(或画树状图)求甲获胜的概率;
(2)你认为这个游戏规则对双方公平吗?请简要说明理由.
相关试题

