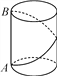
【题目】如图,壁虎在一座底面半径为 2 米,高为 5 米的油罐的下底边沿点 A处,它 发现在自己的正上方油罐上边缘的点 B处有一只害虫,便决定捕捉这只害虫,为了不引起害 虫的注意,它故意不走直线,而是绕着油罐,沿一条螺旋路线,从背后对害虫进行突然袭击.结 果,壁虎偷袭成功,获得了一顿美餐.请问壁虎至少要爬行多少路程 才能捕到害虫?(π取 3)
参考答案:
【答案】壁虎至少要爬行 13 米才能捕到害虫
【解析】试题分析:首先画出如图的圆柱侧面展开图,再连接AB,再根据勾股定理求出AB的长就是壁虎所爬的路程.
试题解析:把这个油罐看成一个圆柱体,再画出它的侧面展开图(是一个长方形)如图所示.

因为A,B 两点间线段最短,所以壁虎至少要爬行线段 AB 这段路程,才能捕捉到害虫.
而 AB2=AC2+BC2=(2π×2) 2+52≈169,
所以 AB=13 米.
答:壁虎至少要爬行 13 米才能捕到害虫.
-
科目: 来源: 题型:
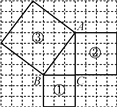
查看答案和解析>>【题目】如图,正方形网格中,每个小正方形的边长都为 1.
(1)正方形①的面积 S1=_________cm2 ,正方形②的面积 S2=______________cm2,正方形③的面积S3=____cm2;
(2)S1,S2,S3之间存在什么关系?
(3)猜想:如果Rt△ABC的三边BC,AC,AB的长分别为a,b,c,那么它们之间存在什么关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】中点、平行线、等腰直角三角形、等边三角形都是常见的几何图形!
(1)如图1,若点D为等腰直角三角形ABC斜边BC的中点,点E、F分别在AB、AC边上,且∠EDF=90°,连接AD、EF,当BC=5
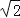 ,FC=2时,求EF的长度;
,FC=2时,求EF的长度;(2)如图2,若点D为等边三角形ABC边BC的中点,点E、F分别在AB、AC边上,且∠EDF=90°;M为EF的中点,连接CM,当DF∥AB时,证明:3ED=2MC;
(3)如图3,若点D为等边三角形ABC边BC的中点,点E、F分别在AB、AC边上,且∠EDF=90°;当BE=6,CF=0.8时,直接写出EF的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 3a3+a3=4a6B. (a+b)2=a2+b2
C. 5a﹣3a=2aD. (﹣a)2a3=﹣a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°∠DAB=45°.(1)求∠DAC的度数;(2)请说明:AB=CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标 ,点B1的坐标 ;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标 .

-
科目: 来源: 题型:
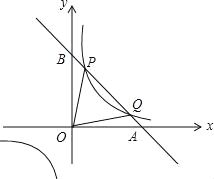
查看答案和解析>>【题目】已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数交于一象限内的P(
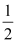 ,n),Q(4,m)两点,且tan∠BOP=
,n),Q(4,m)两点,且tan∠BOP=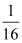 :
:(1)求反比例函数和直线的函数表达式;
(2)求△OPQ的面积.
相关试题

