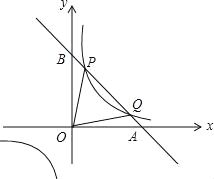
【题目】已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数交于一象限内的P(![]() ,n),Q(4,m)两点,且tan∠BOP=
,n),Q(4,m)两点,且tan∠BOP=![]() :
:
(1)求反比例函数和直线的函数表达式;
(2)求△OPQ的面积.
参考答案:
【答案】(1)直线的函数表达式为y=﹣2x+9;(2)![]() .
.
【解析】
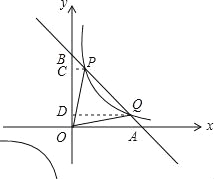
试题分析:(1)过P作PC⊥y轴于C,由P(![]() ,n),得到OC=n,PC=
,n),得到OC=n,PC=![]() ,根据三角函数的定义得到P(
,根据三角函数的定义得到P(![]() ,8),于是得到反比例函数的解析式为y=
,8),于是得到反比例函数的解析式为y=![]() ,Q(4,1),解方程组即可得到直线的函数表达式为y=﹣2x+9;
,Q(4,1),解方程组即可得到直线的函数表达式为y=﹣2x+9;
(2)过Q作OD⊥y轴于D,于是得到S△POQ=S四边形PCDQ=![]() .
.
试题解析:(1)过P作PC⊥y轴于C,∵P(![]() ,n),∴OC=n,PC=
,n),∴OC=n,PC=![]() ,
,
∵tan∠BOP=![]() ,∴n=8,∴P(
,∴n=8,∴P(![]() ,8),设反比例函数的解析式为y=
,8),设反比例函数的解析式为y=![]() ,
,
∴a=4,∴反比例函数的解析式为y=![]() ,∴Q(4,1),
,∴Q(4,1),
把P(![]() ,8),Q(4,1)代入y=kx+b中得
,8),Q(4,1)代入y=kx+b中得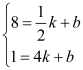 ,∴
,∴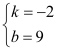 ,
,
∴直线的函数表达式为y=﹣2x+9;
(2)过Q作OD⊥y轴于D,则S△POQ=S四边形PCDQ=![]() (
(![]() +4)×(8﹣1)=
+4)×(8﹣1)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,壁虎在一座底面半径为 2 米,高为 5 米的油罐的下底边沿点 A处,它 发现在自己的正上方油罐上边缘的点 B处有一只害虫,便决定捕捉这只害虫,为了不引起害 虫的注意,它故意不走直线,而是绕着油罐,沿一条螺旋路线,从背后对害虫进行突然袭击.结 果,壁虎偷袭成功,获得了一顿美餐.请问壁虎至少要爬行多少路程 才能捕到害虫?(π取 3)
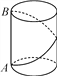
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°∠DAB=45°.(1)求∠DAC的度数;(2)请说明:AB=CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标 ,点B1的坐标 ;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面四个整式中,不能表示图中阴影部分面积的是( )

A.(x+3)(x+2)﹣2x
B.x(x+3)+6
C.3(x+2)+x2
D.x2+5x -
科目: 来源: 题型:
查看答案和解析>>【题目】重庆市旅游文化商店自制了一款文化衫,每件成本价为20元,每天销售150件:
(1)若要每天的利润不低于2250元,则销售单价至少为多少元?
(2)为了回馈广大游客,同时也为了提高这种文化衫的认知度,商店决定在“五一”节当天开展促销活动,若销售单价在(1)中的最低销售价的基础上再降低
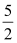 m%,则日销售量可以在150件基础上增加
m%,则日销售量可以在150件基础上增加 m件,结果当天的销售额达到5670元;要使销售量尽可能大,求出m的值.
m件,结果当天的销售额达到5670元;要使销售量尽可能大,求出m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,是同类项的是( )
A.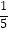
xy2与5x2y
B.3ab3与﹣abc
C.12pq2与﹣8pq2
D.7a与2b
相关试题

