【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(﹣3,3 ![]() ),反比例函数y=
),反比例函数y= ![]() 的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是 .
的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是 . 
参考答案:
【答案】﹣12 ![]()
【解析】解:过点C作CE⊥x轴于点E,

∵顶点C的坐标为(﹣3,3 ![]() ),
),
∴OE=3,CE=3 ![]() ,
,
∴∠BOC=60°,
∵四边形ABOC是菱形,
∴CE⊥x轴于点E= ![]() =6,∠BOD=
=6,∠BOD= ![]() ∠BOC=30°,
∠BOC=30°,
∵DB⊥x轴,
∴DB=OBtan30°=6× ![]() =2
=2 ![]() ,
,
∴点D的坐标为:(﹣6,2 ![]() ),
),
∵反比例函数y= ![]() 的图象与菱形对角线AO交D点,
的图象与菱形对角线AO交D点,
∴k=xy=﹣12 ![]() .
.
所以答案是:﹣12 ![]() .
.
【考点精析】关于本题考查的菱形的性质和解直角三角形,需要了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知
 的平方根是
的平方根是 ,
, 的算术平方根是4,求
的算术平方根是4,求 的值;
的值;(2)若
 与
与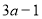 是同一个正数的平方根,求
是同一个正数的平方根,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
 ,点
,点 在射线
在射线 上,
上, .
. 
(1)如图 1,若
 ,求
,求 的度数;
的度数; (2)把“
 °”改为“
°”改为“ ”,射线
”,射线 沿射线
沿射线 平移,得到
平移,得到 ,其它条件不变(如 图 2 所示),探究
,其它条件不变(如 图 2 所示),探究 的数量关系;
的数量关系;(3)在(2)的条件下,作
 ,垂足为
,垂足为 ,与
,与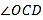 的角平分线
的角平分线 交于点
交于点 ,若
,若 , 用含 α 的式子表示
, 用含 α 的式子表示 (直接写出答案).
(直接写出答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上一动点(不与B,C重合),E是AC上一个动点,始终保持∠ADE=∠B,则当△DCE为直角三角形时,BD的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为每秒1个单位,设运动时间为t秒,过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)在动点P、Q运动的过程中,以B、Q、E为顶点的三角形是直角三角形,直按写出t的值;
(3)设△PEQ的面积为S,求S与时间t的函数关系,并指出自变量t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义符号min{a,b,c}表示a、b、c三个数中的最小值,如min{1,﹣2,3}=﹣2,min{0,5,5}=0.
(1)根据题意填空:min
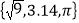 = ;
= ;(2)试求函数y=min{2,x+1,﹣3x+11}的解析式;
(3)关于x的方程﹣x+m=min{2,x+1,﹣3x+11}有解,试求常数m的取值范围.
相关试题

