搜索
【题目】如图，已知△ABC在平面直角坐标系中的位置如图所示，
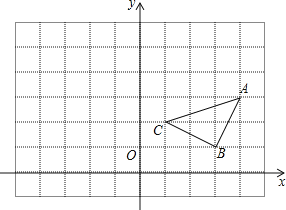
（1）写出△ABC三个顶点的坐标；
（2）求出△ABC的面积；
（3）在图中画出把△ABC先向左平移5个单位，再向上平移2个单位后所得的△A′B′C′，并写出各顶点坐标．
参考答案：
【答案】（1）A（4，3）、B（3，1）、C（1，2）；（2）△ABC的面积为
；（3）如图所示，见解析；△A′B′C′即为所求，A′（﹣1，5）、B′（﹣2，3）、C′（﹣4，4）．
【解析】
（1）由△ABC在平面直角坐标系中的位置可得答案；
（2）利用割补法求解可得答案；
（3）将三个顶点分别向左平移5个单位，再向上平移2个单位得到对应点，继而首尾顺次连接即可得．
解：（1）A（4，3）、B（3，1）、C（1，2）；
（2）△ABC的面积为2×3﹣
×1×2×2﹣×1×3＝；
（3）如图所示，△A′B′C′即为所求，
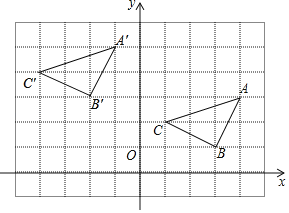
由图知A′（﹣1，5）、B′（﹣2，3）、C′（﹣4，4）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】每年的6月5日为世界环保日，为了提倡低碳环保，某公司决定购买10台节省能源的新设备，现有甲、乙两种型号的设备可供选购. 经调查：购买3台甲型设备比购买2台乙型设备多花16万元，购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格；
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元，你认为该公司有哪几种购买方案；
(3)在（2）的条件下，已知甲型设备的产量为240吨/月，乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨，为了节约资金，请你为该公司设计一种最省钱的购买方案.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：点A在射线CE上，∠C=∠D．
（1）如图1，若AC∥BD，求证：AD∥BC；
（2）如图2，若∠BAC=∠BAD，BD⊥BC，请探究∠DAE与∠C的数量关系，写出你的探究结论，并加以证明；
（3）如图3，在（2）的条件下，过点D作DF∥BC交射线于点F，当∠DFE=8∠DAE时，求∠BAD的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在下列条件中，不能作为判断△ABD≌△BAC的条件是（ )
A. ∠D＝∠C，∠BAD＝∠ABC B. ∠BAD＝∠ABC，∠ABD＝∠BAC
C. BD＝AC，∠BAD＝∠ABC D. AD＝BC，BD＝AC
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在四边形ABCD中，AB=AD. ∠B+∠ADC=180°，点E，F分别在四边形ABCD的边BC，CD上，∠EAF=
∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系.
图1 图2 图3
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG，使AB与AD重合.由∠B+∠ADC=180°，得∠FDG=180°，即点F，D，G三点共线. 易证△AFG
，故EF，BE，DF之间的数量关系为 ；(2)类比引申
如图2，在图1的条件下，若点E，F由原来的位置分别变到四边形ABCD的边CB，DC的延长线上，∠EAF=
∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系，并给出证明.(3)联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D，E均在边BC上，且∠DAE=45°. 若BD=1，EC=2，则DE的长为 .
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，要把残破的轮片复制完整，已知弧上的三点A、B、C.
(1)用尺规作图法找出
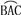所在圆的圆心(保留作图痕迹，不写作法)；(2)设△ABC是等腰三角形，底边BC＝8cm，腰AB＝5cm，求圆片的半径R.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以下各图都是由同样大小的图形①按一定规律组成，其中第①个图形中共有1个完整菱形，第②个图形中共有5个完整菱形，第③个图形中共有13个完整菱形，…，则第⑦个图形中完整菱形的个数为（ ）
A. 83B. 84C. 85D. 86
相关试题
