【题目】一个圆锥的侧面积是2πcm2 , 它的侧面展开图是一个半圆,则这个圆锥的高为cm.
参考答案:
【答案】![]()
【解析】解:设圆锥的母线长为R, π×R2÷2=2π,
解得:R=2,
∴圆锥侧面展开图的弧长为:2π,
∴圆锥的底面圆半径是2π÷2π=1,
∴圆锥的高为 ![]() .
.
所以答案是 ![]() .
.
【考点精析】利用几何体的展开图和圆锥的相关计算对题目进行判断即可得到答案,需要熟知沿多面体的棱将多面体剪开成平面图形,若干个平面图形也可以围成一个多面体;同一个多面体沿不同的棱剪开,得到的平面展开图是不一样的,就是说:同一个立体图形可以有多种不同的展开图;圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h..
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在以O为原点的平面直角坐标系中,点A的坐标为(0,2),点P(s,t)在抛物线y=
 x2+1上,点P到x轴的距离记为m,PA=n.
x2+1上,点P到x轴的距离记为m,PA=n.
(1)若s=4,分别求出m、n的值,并比较m与n的大小关系;
(2)若点P是该抛物线上的一个动点,则(1)中m与n的大小关系是否仍成立?请说明理由;
(3)如图2,过点P的直线y=kx(k≠0)与抛物线交于另一点Q连接PA、QA,是否存在k使得PA=2QA?若存在,请求出k的值;若不存在,请举例说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD的对角线AC,BD相交于点O,AC=4
 ,BD=4,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为S1 , 未被盖住部分的面积为S2 , BP=x.
,BD=4,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为S1 , 未被盖住部分的面积为S2 , BP=x. 
(1)用含x的代数式分别表示S1 , S2;
(2)若S1=S2 , 求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(2,2)关于直线y=k
 (k>0)的对称点恰好落在x轴的正半轴上,则k的值是_____.
(k>0)的对称点恰好落在x轴的正半轴上,则k的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线lAC:y=﹣
 交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.
交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.(1)求点B的坐标及直线BC的解析式;
(2)将△OBC关于BC边翻折,得到△O′BC,过点O′作直线O′E垂直x轴于点E,F是y轴上一点,P是直线O′E上任意一点,P、Q两点关于x轴对称,当|PA﹣PC|最大时,请求出QF+
 FC的最小值;
FC的最小值;(3)若M是直线O′E上一点,且QM=3
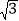 ,在(2)的条件下,在平面直角坐标系中,是否存在点N,使得以Q、F、M、N四点为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
,在(2)的条件下,在平面直角坐标系中,是否存在点N,使得以Q、F、M、N四点为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
相关试题

