【题目】如图,已知直线lAC:y=﹣![]() 交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.
交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.
(1)求点B的坐标及直线BC的解析式;
(2)将△OBC关于BC边翻折,得到△O′BC,过点O′作直线O′E垂直x轴于点E,F是y轴上一点,P是直线O′E上任意一点,P、Q两点关于x轴对称,当|PA﹣PC|最大时,请求出QF+![]() FC的最小值;
FC的最小值;
(3)若M是直线O′E上一点,且QM=3![]() ,在(2)的条件下,在平面直角坐标系中,是否存在点N,使得以Q、F、M、N四点为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
,在(2)的条件下,在平面直角坐标系中,是否存在点N,使得以Q、F、M、N四点为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)B(6,0);y=![]() x﹣2
x﹣2![]() ;(2)5
;(2)5![]() ;(3)(6,3
;(3)(6,3![]() )或(0,
)或(0,![]() )或(0,7
)或(0,7![]() )或(6,9
)或(6,9![]() ).
).
【解析】
(1)利用待定系数法求出A、C两点坐标,再根据两直线垂直k的乘积为-1,求出直线BC的解析式即可解决问题;
(2)首先证明∠ACO=30°,如图,作QH⊥AC于H,交y轴于F.则FH=![]() CF,根据垂线段最短可知,QF+
CF,根据垂线段最短可知,QF+![]() FC的最小值为线段HQ的长;
FC的最小值为线段HQ的长;
(3)求出点M坐标分两种情形分别讨论求解即可.
解:(1)由题意A(﹣2,0),C(0,﹣2![]() ),
),
∵直线lAC:y=﹣![]() ,BC⊥AC,
,BC⊥AC,
∴直线BC的解析式为y=![]() x﹣2
x﹣2![]() ,
,
令y=0,解得x=6,
∴B(6,0).
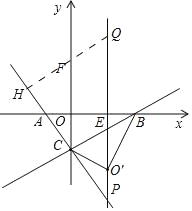
(2)∵△OBC关于BC边翻折,得到△O′BC,
∴可得O′(3,﹣3![]() ),
),
当|PA﹣PC|最大时,点P在直线AC上,此时P(3,﹣5![]() ),
),
∵P、Q关于x轴对称,
∴Q(3,5![]() ),
),
在Rt△AOC中,∵tan∠ACO=![]() =
=![]() ,
,
∴∠ACO=30°,
如图,作QH⊥AC于H,交y轴于F.
则FH=![]() CF,
CF,
根据垂线段最短可知,QF+![]() FC的最小值为线段HQ的长,
FC的最小值为线段HQ的长,
在Rt△PQH中,∵∠HPQ=∠ACO=30°,PQ=10![]() ,
,
∴HQ=![]() PQ=5
PQ=5![]() ,
,
∴QF+![]() FC的最小值为5
FC的最小值为5![]() .
.
(3)由(2)可知:F(0,4![]() ),
),
∵QM=3![]() ,
,
∴M(3,2![]() )或(3,8
)或(3,8![]() ),
),
当M(3,2![]() )时,如图,以Q、F、M、N四点为顶点的四边形是平行四边形,可得满足条件的点N坐标为(6,3
)时,如图,以Q、F、M、N四点为顶点的四边形是平行四边形,可得满足条件的点N坐标为(6,3![]() )或(0,
)或(0,![]() )或(0,7
)或(0,7![]() ),
),
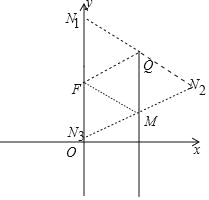
当M为(3,8![]() )时,同法可得满足条件的点N坐标为(6,9
)时,同法可得满足条件的点N坐标为(6,9![]() )或(0,7
)或(0,7![]() )或(0,
)或(0,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆锥的侧面积是2πcm2 , 它的侧面展开图是一个半圆,则这个圆锥的高为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将边长为2的正方形OABC如图放置,O为原点.若∠α=15°,则点B的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】复习课中,教师给出关于x的函数y=2kx2﹣(4k+1)x﹣k+1(k是实数).
教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.
学生思考后,黑板上出现了一些结论.教师作为活动一员,又补充一些结论,并从中选出以下四条:
①存在函数,其图象经过(1,0)点;
②函数图象与坐标轴总有三个不同的交点;
③当x>1时,不是y随x的增大而增大就是y随x的增大而减小;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数.
教师:请你分别判断四条结论的真假,并给出理由.最后简单写出解决问题时所用的数学方法. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列做法正确的是( )
A. 方程
 =1+
=1+ 去分母,得2(2x-1)=1+3(x-3)
去分母,得2(2x-1)=1+3(x-3)B. 方程4x=7x-8移项,得4x-7x=8
C. 方程3(5x-1)-2(2x-3)=7去括号,得15x-3-4x-6=7
D. 方程1-
 x=3x+
x=3x+ 移项,得-
移项,得- x-3x=
x-3x= -1
-1 -
科目: 来源: 题型:
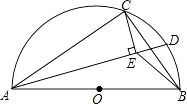
查看答案和解析>>【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是 .
相关试题

