【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
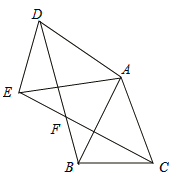
(1)求证:![]() ;
;
(2)若AB=2,![]() ,当四边形ADFC是菱形时,求BF的长。
,当四边形ADFC是菱形时,求BF的长。
参考答案:
【答案】(1)证明过程见解析;(2)BF=2![]() -2
-2
【解析】
(2)试题分析:(1)根据△ABC≌△ADE得出AE=AD,∠BAC=∠DAE,从而得出∠CAE=∠DAB,根据SAS判定定理得出三角形全等;(2)根据菱形的性质得出∠DBA=∠BAC=45°,根据AB=AD得出△ABD是直角边长为2的等腰直角三角形,从而得出BD=2![]() ,根据菱形的性质得出AD=DF=FC=AC=AB=2,最后根据BF=BD-DF求出答案.
,根据菱形的性质得出AD=DF=FC=AC=AB=2,最后根据BF=BD-DF求出答案.
试题解析:(1)∵△ABC≌△ADE且AB=AC ∴AE=AD,AB=AC
∠BAC+∠BAE=∠DAE+∠BAE ∴∠CAE=∠DAB ∴△AEC≌△ADB
(3)∵四边形ADFC是菱形且∠BAC=45° ∴∠DBA=∠BAC=45° 由(1)得AB=AD
∴∠DBA=∠BDA=45° ∴△ABD是直角边长为2的等腰直角三角形 ∴BD=2![]()
又∵四边形ADFC是菱形 ∴AD=DF=FC=AC=AB=2 ∴BF=BD-DF=2![]() -2
-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,2014年全国约有939万人参加高考,939万人用科学记数法表示为____________人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=2x2+4x-5用配方法转化为y=a(x-h)2+k的形式是________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定两数a,b之间的一种运算,记作(a,b):如果
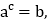
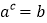 ,那么(a,b)=c.
,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)=_______,(5,1)=_______,(2,
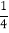
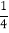 )=_______.
)=_______.(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为
 (分),且
(分),且 ,将其按分数段分为五组,绘制出以下不完整表格:
,将其按分数段分为五组,绘制出以下不完整表格:组别
成绩
 (分)
(分)频数(人数)
频率
一

2
0.04
二

10
0.2
三
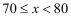
14
b
四

a
0.32
五

8
0.16
请根据表格提供的信息,解答以下问题: (1)本次决赛共有 名学生参加;
(2)直接写出表中a= ,b= ;
(3)请补全下面相应的频数分布直方图;

(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作☉O,交BD于点E,连接CE,过D作DF
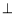 AB于点F,∠BCD=2∠ABD.
AB于点F,∠BCD=2∠ABD.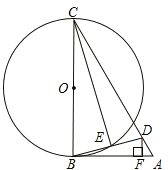
(1)求证:AB是☉O的切线;
(2)若∠A=60°,DF=
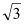 ,求☉O的直径BC的长。
,求☉O的直径BC的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】菱形两条对角线长为8cm和6cm,则菱形面积为_____cm2.
相关试题

