【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
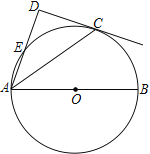
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1) 详见解析;(2)![]() .
.
【解析】试题分析:(1) 连接OC,由已知条件易得∠CAD=∠OCA,∠OCA=∠OAC,所以∠CAD=∠CAO,即可得AC平分∠DAB;(2).连接BE交OC于点H,易证OC⊥BE,可知∠OCA=∠CAD,因COS∠HCF=![]() ,可设HC=4,FC=5,则FH=3.由△AEF∽△CHF,设EF=3x,则AF=5x,AE=4x,所以OH=2x ,在△OBH中,由勾股定理列方程求解即可.
,可设HC=4,FC=5,则FH=3.由△AEF∽△CHF,设EF=3x,则AF=5x,AE=4x,所以OH=2x ,在△OBH中,由勾股定理列方程求解即可.
试题解析:(1)证明:连接OC,则OC⊥CD,
又AD⊥CD,
∴AD∥OC,
∴∠CAD=∠OCA,
又OA=OC,∴∠OCA=∠OAC,
∴∠CAD=∠CAO,
∴AC平分∠DAB.
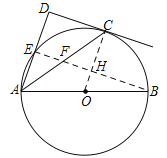
(2)解:连接BE交OC于点H,易证OC⊥BE,可知∠OCA=∠CAD,
∴COS∠HCF=![]() ,设HC=4,FC=5,则FH=3.
,设HC=4,FC=5,则FH=3.
又△AEF∽△CHF,设EF=3x,则AF=5x,AE=4x,∴OH=2x
∴BH=HE=3x+3 OB=OC=2x+4
在△OBH中,(2x)2+(3x+3)2=(2x+4)2
化简得:9x2+2x-7=0,解得:x=![]() (另一负值舍去).
(另一负值舍去).
∴![]() .
.
-
科目: 来源: 题型:
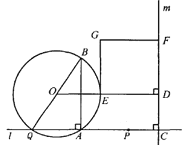
查看答案和解析>>【题目】(本题14分)如图,点A和动点P在直线
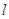 上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线
上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线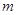 ⊥
⊥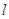 ,过点O作OD⊥
,过点O作OD⊥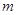 于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=
于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=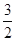 CD,以DE,DF为邻边作矩形DEGF,设AQ=
CD,以DE,DF为邻边作矩形DEGF,设AQ=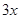
(1)用关于
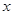 的代数式表示BQ,DF;
的代数式表示BQ,DF;(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长;
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于另一点N,若BN的弦心距为1,求AP的长(直接写出答案)
-
科目: 来源: 题型:
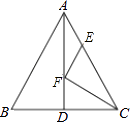
查看答案和解析>>【题目】如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
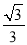 x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此作法进行下去,则OA2017=_____.
x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此作法进行下去,则OA2017=_____.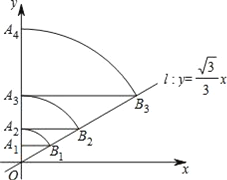
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
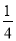 x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.
x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.(1)求抛物线的解析式;
(2)若PA:PB=3:1,求一次函数的解析式;
(3)在(2)的条件下,当k>0时,抛物线的对称轴上是否存在点C,使得⊙C同时与x轴和直线AP都相切,如果存在,请求出点C的坐标,如果不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果长方形的周长为4m,一边长为m﹣n,则另一边长为( )
A.3m+n
B.2m+2n
C.m+n
D.m+3n -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+3x=0的根的说法正确的是( )
A.没有实数根
B.只有一个实数根
C.有两个相等的实数根
D.有两个不相等的实数根
相关试题

