【题目】如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 . 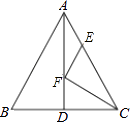
参考答案:
【答案】![]()
【解析】解:作BE⊥AC垂足为E,交AD于F,此时CF+EF最小.
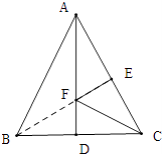
理由如下:∵AB=AC,AD是中线,
∴AD⊥BC,
∴FB=FC,
∴CF+EF=BF+EF,
∵线段BE是垂线段,根据垂线段最短,
∴点E、点F、就是所找的点.
∵ ![]() BCAD=
BCAD= ![]() ACBE,
ACBE,
∴ ![]() ×20×24=
×20×24= ![]() ×26×BE,
×26×BE,
∴BE= ![]() ,
,
∴CF+EF的最小值=BE= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】本题主要考查了三角形的面积和线段垂直平分线的性质的相关知识点,需要掌握三角形的面积=1/2×底×高;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把方程2x+y=3改写成用含x的式子表示y的形式,得y= .
-
科目: 来源: 题型:
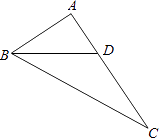
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,那么点D到BC的距离是 .
-
科目: 来源: 题型:
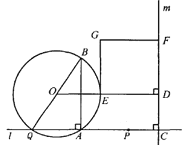
查看答案和解析>>【题目】(本题14分)如图,点A和动点P在直线
 上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线
上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线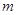 ⊥
⊥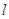 ,过点O作OD⊥
,过点O作OD⊥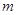 于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=
于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=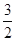 CD,以DE,DF为邻边作矩形DEGF,设AQ=
CD,以DE,DF为邻边作矩形DEGF,设AQ=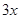
(1)用关于
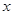 的代数式表示BQ,DF;
的代数式表示BQ,DF;(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长;
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于另一点N,若BN的弦心距为1,求AP的长(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
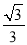 x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此作法进行下去,则OA2017=_____.
x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此作法进行下去,则OA2017=_____.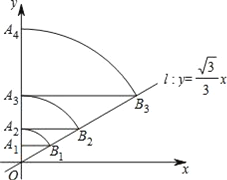
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
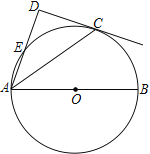
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=
 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.
x2+mx+n的图象经过点A(2,3),对称轴为直线x=1,一次函数y=kx+b的图象经过点A,交x轴于点P,交抛物线于另一点B,点A、B位于点P的同侧.(1)求抛物线的解析式;
(2)若PA:PB=3:1,求一次函数的解析式;
(3)在(2)的条件下,当k>0时,抛物线的对称轴上是否存在点C,使得⊙C同时与x轴和直线AP都相切,如果存在,请求出点C的坐标,如果不存在,请说明理由.

相关试题

