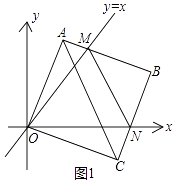
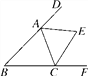
【题目】在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点,现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).
(1)旋转过程中,当MN和AC平行时,求正方形OABC旋转的角度;
(2)试证明旋转过程中,△MNO的边MN上的高为定值;
(3)折△MBN的周长为p,在旋转过程中,p值是否发生变化?若发生变化,说明理由;若不发生变化,请给予证明,并求出p的值.
参考答案:
【答案】
(1)
解:如图1中,
∵四边形OABC是正方形,
∴∠BAC=∠BCA=45°,BA=BC,OA=OC,∠OAB=∠OCB=90°
∵MN∥AC,
∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°,
∴∠BMN=∠BNM.
∴BM=BN,
∴AM=CN.
在△OAM与△OCN中,
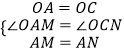
∴△OAM≌△OCN(SAS),
∴∠AOM=∠CON,
∴∠AOM=∠CON=22.50,
∴MN∥AC时,旋转角为22.50.
(2)
解:证明:如图2中,
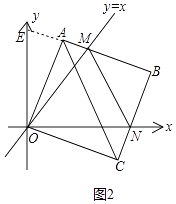
过点O作OF⊥MN于F,延长BA交y轴与E点,则∠AOE=45°﹣∠AOM,∠CON=45°﹣∠AOM.
∴∠AOE=∠CON.
在△OAE与△OCN中,
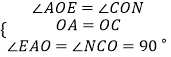
∴△OAE≌△OCN(ASA),
∴OE=ON,AE=CN.
在△OME与△OMN中,
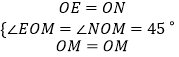
∴△OME≌△OMN(SAS),
∴∠OME=∠OMN.
∵MA⊥OA,MF⊥OF.
∴OA=OF=2,
∴在旋转过程中,高为定值.
(3)
解:旋转过程中,p值不变化.
理由:∵△OME≌△OMN,
∴ME=MN,
∵AE=CN,
∴MN=ME﹣AM+AE=AM+CN.
∴p=MN+BN+BM=AM+CN+BN+BM=AB+AC=4.
∴△MBN的周长p为定值.
【解析】(1)只要证明△AOM≌△CON,推出∠AOM=∠CON=22.5°即可解决问题.(2)如图2中,过点O作OF⊥MN于F,延长BA交y轴与E点,则∠AOE=45°﹣∠AOM,∠CON=45°﹣∠AOM.先证明△OAE≌△OCN(ASA),再证明△OME≌△OMN(SAS),推出∠OME=∠OMN,利用角平分线性质定理即可解决问题.(3)由(2)可知,MN=AM+CN,可以推出△BMN的周长为BA+BC是定值.
【考点精析】本题主要考查了图形的旋转的相关知识点,需要掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).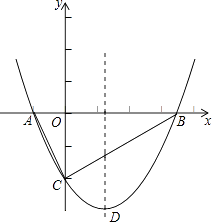
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】具备下列条件的三角形ABC中,不为直角三角形的是( )
A.∠A+∠B=∠C B.∠A=∠B=
 ∠C
∠CC.∠A=90°﹣∠B D.∠A﹣∠B=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=1,y=
 ,则x2+4xy+4y2的值是( )
,则x2+4xy+4y2的值是( )A. 2 B. 4 C. 32 D. 12
【答案】B
【解析】解析:x2+4xy+4y2=(x+2y)2=
 =4.故选B.
=4.故选B.【题型】单选题
【结束】
9【题目】下列因式分解,正确的是( )
A. x2y2-z2=x2(y+z)(y-z) B. -x2y+4xy-5y=-y(x2+4x+5)
C. (x+2)2-9=(x+5)(x-1) D. 9-12a+4a2=-(3-2a)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=
 x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣  )x+c=0(a≠0)的根的情况( )
)x+c=0(a≠0)的根的情况( ) 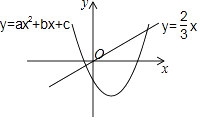
A.两根都大于0
B.两根都等于0
C.两根都小于0
D.一根大于0,一根小于0 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x
 .
.(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若
 ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;(3)当
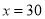 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠B=46°,△ABC的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为________.
相关试题

