【题目】将正方形ABCD(如图1)作如下划分:第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;第2次划分:将图2左上角正方形AEMH按上述方法再作划分,得图3,则图3中共有_________个正方形;若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有_______个正方形;继续划分下去,能否将正方形ABCD划分成有2011个正方形的图形?需说明理由.

参考答案:
【答案】9,401,不能理由见解析.
【解析】
本题需先根据图形,得出第2次划分共有多少个正方形,找出规律,得出n个的时候有多少个,从而得出结果.
∵第一次划分,得出5个正方形,
∴第2次划分,根据图形得出共有9个正方形;
∴依题意得:第n次划分后,图中共有4n+1个正方形
∴第100次划分后,共有401个正方形;
∵第n次划分后,图中共有4n+1个正方形,
∴方程4n+1=2011没有整数解,
∴不能得到2011个正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,则△DCE的面积为( )

A.
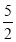 B.
B.  C. 2D. 1
C. 2D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】我市公共自行车服务公司调查某中学学生对公共自行车的了解情况,随机抽取部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图.

(1)本次问卷共随机调查了 名学生,扇形统计图中
 .
.(2)请根据数据信息补全条形统计图,并求扇形统计图中“D类型”所对应的圆心角.
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在矩形纸片
,在矩形纸片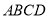 中,
中, ,
,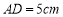 ,折叠纸片使
,折叠纸片使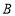 点落在边
点落在边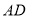 上的
上的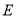 处,折痕为
处,折痕为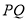 .过点
.过点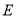 作
作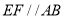 交
交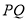 于
于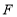 ,连接
,连接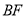 .
.(1)求证:四边形
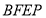 为菱形;
为菱形;(2)当点
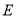 在
在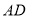 边上移动时,折痕的端点
边上移动时,折痕的端点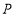 ,
,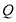 也随之移动.
也随之移动.①当点
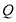 与点
与点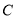 重合时(如图
重合时(如图 ),求菱形
),求菱形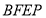 的边长;
的边长;②若限定
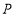 ,
,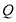 分别在边
分别在边 ,
, 上移动,求出点
上移动,求出点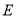 在边
在边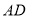 上移动的最大距离.
上移动的最大距离.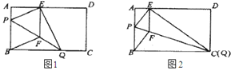
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是甲、乙两班参加“学法、用法知识竞赛”活动中各题答对人数的折线统计图,下列结论错误的是( )

A. 甲班答对第二题和第五题的人数相等
B. 甲班答对第三题的人数和乙班答对第三题的人数相等
C. 甲班答对第四题的人数比乙班答对第四题的人数少2人
D. 甲班答对各题的人数都比乙班的多
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果经销商上月份销售一种新上市的水果,平均售价为10元/千克,月销售量为1000千克.经市场调查,若将该种水果价格调低至x元/千克,则本月份销售量y(千克)与x(元/千克)之间符合一次函数关系,并且得到了表中的数据:
价格x(元/千克)
7
5
价格y(千克)
2000
4000
(1)求y与x之间的函数解析式;
(2)已知该种水果上月份的成本价为5元/千克,本月份的成本价为4元/千克,要使本月份销售该种水果所获利润比上月份增加20%,同时又要让顾客得到实惠,那么该种水果价格每千克应调低至多少元?
相关试题

