【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,BD=4cm,CD=2cm,
(1)求D点到直线AB的距离.
(2)求AC.

参考答案:
【答案】(1)2cm;(2)2![]() .
.
【解析】
(1)作DE⊥AB,由角平分线的性质知CD=DE=2,故为D点到直线AB的距离;
(2)∵BD=4,DE=2,∠BED=90°,故∠B=30°,
再根据BC=6,AB=2AC与勾股定理即可求出AC的长.
(1)作DE⊥AB,
∵AD平分∠CAB,DE⊥AB,CD⊥AC
∴CD=DE=2,故为D点到直线AB的距离;
(2)∵BD=4,DE=2,∠BED=90°,
∴∠B=30°,
∴AB=2AC
设AC=x,则AB=2x,
由AB2=AC2+BC2,
(2x)2=x2+62,
解得x=2![]() .
.
-
科目: 来源: 题型:
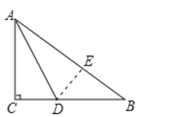
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线AB与y轴交于点
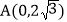 ,与x轴交于点B,
,与x轴交于点B,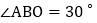 ,直线CD与y轴交于点D,与x轴交于点
,直线CD与y轴交于点D,与x轴交于点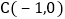 ,
,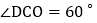 ,直线AB与直线CD交于点Q,E为直线CD上一动点,过点E作x轴的垂线,交直线AB于点M,交x轴于点N,连接AE、BE.
,直线AB与直线CD交于点Q,E为直线CD上一动点,过点E作x轴的垂线,交直线AB于点M,交x轴于点N,连接AE、BE. 求直线AB、CD的解析式及点Q的坐标;
求直线AB、CD的解析式及点Q的坐标; 当E点运动到Q点的右侧,且
当E点运动到Q点的右侧,且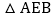 的面积为
的面积为 时,在y轴上有一动点P,直线AB上有一动点R,当
时,在y轴上有一动点P,直线AB上有一动点R,当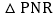 的周长最小时,求点P的坐标及
的周长最小时,求点P的坐标及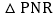 周长的最小值.
周长的最小值.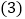 在
在 问的条件下,如图2将
问的条件下,如图2将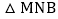 绕着点B逆时针旋转
绕着点B逆时针旋转 得到
得到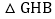 ,使点M与点G重合,点N与点H重合,再将
,使点M与点G重合,点N与点H重合,再将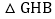 沿着直线AB平移,记平移中的
沿着直线AB平移,记平移中的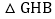 为
为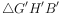 ,在平移过程中,设直线
,在平移过程中,设直线 与x轴交于点F,是否存在这样的点F,使得
与x轴交于点F,是否存在这样的点F,使得 为等腰三角形?若存在,求出此时点F的坐标;若不存在,说明理由
为等腰三角形?若存在,求出此时点F的坐标;若不存在,说明理由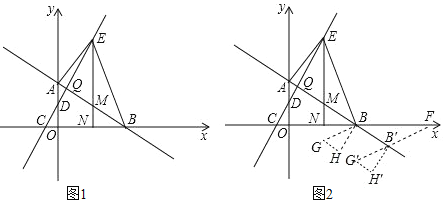
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场正在销售帐篷和棉被两种防寒商品,已知购买
 顶帐篷和
顶帐篷和  床棉被共需
床棉被共需  元,购买
元,购买  顶帐篷和
顶帐篷和  床棉被共需
床棉被共需  元.
元.(1)求
 顶帐篷和
顶帐篷和  床棉被的价格各是多少元?
床棉被的价格各是多少元?(2)某学校准备购买这两种防寒商品共
 件,送给青海玉树灾区,要求每种商品都要购买,且帐篷的数量多于棉被的数量,但因为学校资金不足,购买总金额不能超过
件,送给青海玉树灾区,要求每种商品都要购买,且帐篷的数量多于棉被的数量,但因为学校资金不足,购买总金额不能超过  元,请问学校共有几种购买方案?(要求写出具体的购买方案)
元,请问学校共有几种购买方案?(要求写出具体的购买方案) -
科目: 来源: 题型:
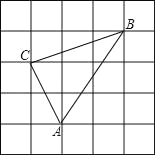
查看答案和解析>>【题目】如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)边AC,AB,BC的长;
(2)点C到AB边的距离;
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=﹣
 x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的函数解析式是( )
x+8与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的函数解析式是( )
A. y=﹣
 x+8 B. y=﹣
x+8 B. y=﹣ x+8 C. y=﹣
x+8 C. y=﹣ x+3 D. y=﹣
x+3 D. y=﹣ x+3
x+3 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校九年级学生的理化实验操作情况,随机抽查了
 名同学实验操作的得分(满分10分).根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:
名同学实验操作的得分(满分10分).根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:
(1)扇形①的圆心角的大小是 ;
(2)求这个样本的容量和样本数据的平均数;
(3)若该校九年级共有
 名学生,估计该校理化实验操作得满分的学生有多少人.
名学生,估计该校理化实验操作得满分的学生有多少人. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:对于二次三项式
 ,能直接用公式法进行因式分解,得到
,能直接用公式法进行因式分解,得到  ,但对于二次三项式
,但对于二次三项式  ,就不能直接用公式法了.我们可以采用这样的方法:在二次三项式
,就不能直接用公式法了.我们可以采用这样的方法:在二次三项式  中先加上一项
中先加上一项  ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去  这项,使整个式子的值不变,于是:
这项,使整个式子的值不变,于是:
像这样把二次三项式分解因式的方法叫做添(拆)项法.
 问题解决:请用上述方法将二次三项式
问题解决:请用上述方法将二次三项式  分解因式.
分解因式.(2)拓展应用:二次三项式
 有最小值或有最大值吗?如果有,请你求出来并说明理由.
有最小值或有最大值吗?如果有,请你求出来并说明理由.
相关试题

