【题目】如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( ) 
A.π﹣2
B.2π﹣2
C.4π﹣4
D.4π﹣8
参考答案:
【答案】A
【解析】解:连接OC∵在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是 ![]() 的中点, ∴∠COD=45°,
的中点, ∴∠COD=45°,
∴OC= ![]() CD=2
CD=2 ![]() ,
,
∴阴影部分的面积=扇形BOC的面积﹣三角形ODC的面积
= ![]() ×π×(2
×π×(2 ![]() )2﹣
)2﹣ ![]() ×22
×22
=π﹣2.
故选:A.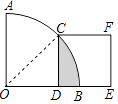
【考点精析】掌握正方形的性质和扇形面积计算公式是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专买店销售A,B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的件价各为多少万元;
每辆A型车和B型车的售价分别是x万元,y万元.
根据题意,列方程组
解这个方程组,得x= ,y=
答: .
(2)有一家公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不超过130万元,求这次购进B型车最多几辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.

(1)求证:BD=BE;
(2)若DBC=30,CD=4,求四边形ABED的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C,点D是抛物线的顶点.

(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点,(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线y=﹣x2+bx+c上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库。已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨。从甲、乙两库到A、B两库的路程和运费如下表(表中“元/吨·千米”表示每吨粮食运送1千米所需人民币)
路程(千米)
运费(元/吨·千米)
甲库
乙库
甲库
乙库
A库
20
15
12
12
B库
25
20
10
8
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点C在∠AOB的一边OA上,过点C的直线DE∥O B.做∠ACD的平分线CF,过点C画CF的垂线CG,如图所示.
(Ⅰ)若∠AOB=40°,求∠ACD及∠ECF的度数;
(Ⅱ)求证:CG平分∠OCD;
(Ⅲ)延长FC交OB于点H,用直尺和三角板过点O作OR⊥FH,垂足为R,过点O
作FH的平行线交ED于点Q.先补全图形,再证明∠COR=∠GCO,∠CQO=∠CHO.

-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究与应用:

(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分面积是 (写成两数平方差的形式)
(2)小颖将阴影部分裁下来,重新拼成一个长方形,如图乙,则长方形的长是 ,宽是 ,面积是 (写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到公式 (用式子表达)
(4)运用你所得到的公式计算:10.3×9.7.
相关试题

