【题目】如图1,二次函数y= ![]() x2+bx+c与一次函数y=
x2+bx+c与一次函数y= ![]() x﹣3的图象都经过x轴上点A(4,0)和y轴上点B(0,﹣3),过动点M(m,0)(0<m<4)作x轴的垂线交直线AB于点C,交抛物线于点P.
x﹣3的图象都经过x轴上点A(4,0)和y轴上点B(0,﹣3),过动点M(m,0)(0<m<4)作x轴的垂线交直线AB于点C,交抛物线于点P.
(1)求b,c的值;
(2)点M在运动的过程中,能否使△PBC为直角三角形?如果能,求出点P的坐标;如果不能,请说明理由;
(3)如图2,过点P作PD⊥AB于点,设△PCD的面积为S1 , △ACM的面积为2 , 若 ![]() =
= ![]() ,
,
①求m的值;
②如图3,将线段OM绕点O顺时针旋转得到OM′,旋转角为α(0°<α<90°),连接M'A、M'B,求M'A+ ![]() M'B的最小值.
M'B的最小值.
参考答案:
【答案】
(1)
解:由题意, ![]() ,
,
解得 
(2)
解:若△PBC为直角三角形,显然∠PCB≠90°.
①当∠PBC=90°时(如图1﹣1中),作PK⊥y轴于K,则∠PBK=∠BAO=90°﹣∠ABO,
∴tan∠PBK= ![]() =
= ![]() ,
,
解得m= ![]() 或0(舍弃),
或0(舍弃),
∴P( ![]() ,﹣
,﹣ ![]() ),
),
②当∠BPC=90°时(如图1﹣2中),BP∥x轴,
当y=﹣3时, ![]() m2﹣
m2﹣ ![]() m﹣3=﹣3,解得m=3或0(舍弃),
m﹣3=﹣3,解得m=3或0(舍弃),
∴P(3,﹣3),
综上所述,满足条件的点P坐标( ![]() ,﹣
,﹣ ![]() )或(3,﹣3)
)或(3,﹣3)

(3)
解:①如图2中,

∵PD⊥AB,PM⊥OA,
∴∠PDC=∠AMC,
∵∠PCD=∠ACM,
∴△PCD∽△ACM,
∴ ![]() =(
=( ![]() )2=
)2= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵CM∥OB,
∴ ![]() =
= ![]() ,
,
∴AC= ![]() (4﹣m),
(4﹣m),
∵抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣3,
x﹣3,
∴PC= ![]() m﹣3﹣(
m﹣3﹣( ![]() m2﹣
m2﹣ ![]() m﹣3)=﹣
m﹣3)=﹣ ![]() m2+3m,
m2+3m,
∴  =
= ![]() ,
,
解得m=2或4(舍弃),
∴m=2.
②如图3中,在y轴上取一点E,使得OE= ![]() ,连接M′E,AE.
,连接M′E,AE.

∵OM′=2,OEOB= ![]() ×3=4,
×3=4,
∴OM2=OEOB,
∴ ![]() =
= ![]() ,
,
∵∠M′OE=∠BOM′,
∴△M′OE∽△BOM′,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴M′E= ![]() BM′,
BM′,
∴AM′+ ![]() BM′=AM′+M′E,
BM′=AM′+M′E,
∴当A、M′、E共线时,AM′+ ![]() BM′的值有最小值=AE=
BM′的值有最小值=AE= ![]() =
= ![]()
![]()
【解析】(1)利用待定系数法即可解决问题.(2)分两种情形讨论即可.①当∠PBC=90°时(如图1﹣1中),作PK⊥y轴于K.②当∠BPC=90°时(如图1﹣2中),BP∥x轴.分别列出方程即可解决问题.(3)①由△PCD∽△ACM,可得 ![]() =(
=( ![]() )2=
)2= ![]() ,推出
,推出 ![]() =
= ![]() ,由CM∥OB,推出
,由CM∥OB,推出 ![]() =
= ![]() ,推出AC=
,推出AC= ![]() (4﹣m),由抛物线的解析式为y=
(4﹣m),由抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣3,可得PC=
x﹣3,可得PC= ![]() m﹣3﹣(
m﹣3﹣( ![]() m2﹣
m2﹣ ![]() m﹣3)=﹣
m﹣3)=﹣ ![]() m2+3m,列出方程,即可解决问题.②如图3中,在y轴上取一点E,使得OE=
m2+3m,列出方程,即可解决问题.②如图3中,在y轴上取一点E,使得OE= ![]() ,连接M′E,AE.由OM′=2,OEOB=
,连接M′E,AE.由OM′=2,OEOB= ![]() ×3=4,推出OM2=OEOB,推出
×3=4,推出OM2=OEOB,推出 ![]() =
= ![]() ,由∠M′OE=∠BOM′,可知△M′OE∽△BOM′,推出
,由∠M′OE=∠BOM′,可知△M′OE∽△BOM′,推出 ![]() =
= ![]() =
= ![]() ,推出M′E=
,推出M′E= ![]() BM′,所以AM′+
BM′,所以AM′+ ![]() BM′=AM′+M′E,所以当A、M′、E共线时,AM′+
BM′=AM′+M′E,所以当A、M′、E共线时,AM′+ ![]() BM′的值有最小值.
BM′的值有最小值.
【考点精析】掌握二次函数的性质和相似三角形的应用是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ,
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=6,BC=10,AB的垂直平分线分别交BC、AB于点D、E.
(1)求△ACD的周长;
(2)若∠C=25°,求∠CAD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】三角板是学习数学的重要工具,将一副三角板中的两块直角三角板的直角顶点
 按如图方式叠放在一起,当
按如图方式叠放在一起,当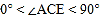 且点
且点 在直线
在直线 的上方时,解决下列问题:(友情提示:
的上方时,解决下列问题:(友情提示: ,
, ,
, .
.
(1)①若
 ,则
,则 的度数为 ;
的度数为 ;②若
 ,则
,则 的度数为 ;
的度数为 ;(2)由(1)猜想
 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.(3)这两块三角板是否存在一组边互相平行?若存在,请直接写出
 的角度所有可能的值(不必说明理由);若不存在,请说明理由.
的角度所有可能的值(不必说明理由);若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长.如图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长超过13小时的节气是( )

A.惊蛰
B.小满
C.秋分
D.大寒
相关试题

