【题目】(1)计算(2a+1)2﹣(2a+1)(﹣1+2a);
(2)用乘法公式计算:20022﹣2001×2003;
(3)解不等式组: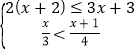 ,并把解集在数轴上表示出来;
,并把解集在数轴上表示出来;
(4)解方程组: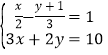 .
.
参考答案:
【答案】(1)4a+2;(2)1;(3)1≤x<3;(4)![]() .
.
【解析】分析(1)原式第一项利用完全平方公式展开,第二项利用平方差公式化简,去括号合并即可得到结果;
(2)原式变形后,利用平方差公式计算即可得到结果;
(3)分别求出不等式组中两不等式的解集,找出解集的公共部分即可;
(4)方程组变形后,利用加减消元法求出解即可.
:(1)原式=4a2+4a+1﹣4a2+1
=4a+2;
(2)原式=20022﹣(2002﹣1)×(2002+1)=20022﹣20022+1=1;
(3)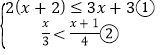 ,
,
由①得:x≥1;
由②得:x<3,
则不等式组的解集为 1≤x<3,
把解集在数轴上表示出来为:![]()
(4)方程组整理得: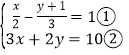 ,
,
①+②得:6x=18,即 x=3,
将 x=3 代入①得:y=![]() ,
,
则方程组的解为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=7,AC=
 ,∠A=45°,AH⊥HC,垂足为H。
,∠A=45°,AH⊥HC,垂足为H。(1)求证:△AHC是等腰直角三角形;
(2)求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条笔直地公路上有A,B,C三地,,两地相距150km,甲、乙两辆汽车分别从B,C两地同时出发,沿公路匀速相向而行,分别驶往C,B两地.甲、乙两车到A地的距离y1,y2与行驶时间x(h)的函数图象如图2所示.(乙:折线)
(1)请在图1中标出A地的大致位置;
(2)图2中,M点的坐标是_________,该点的实际意义是_________;
(3)求甲车到A地的距离
 与行驶时间
与行驶时间 的函数关系式,直接写出乙车到A地的距离y2与行驶时间
的函数关系式,直接写出乙车到A地的距离y2与行驶时间 的函数关系式,并在图2中补全甲车的函数图象;
的函数关系式,并在图2中补全甲车的函数图象;(4)A地设有指挥中心,指挥中心与两车配有对讲机,两部对讲机在之15km内(含15km)时能够互相通话,直接写出两车可以同时与指挥中心用对讲机通话的时间.


-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件)
n=50﹣x
销售单价m(元/件)
当1≤x≤20时,m=20+
 x
x当21≤x≤30时,m=10+
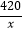
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0).
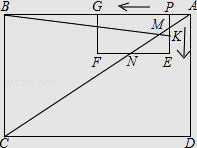
(1)当t=1时,KE= , EN=;
(2)当t为何值时,△APM的面积与△MNE的面积相等?
(3)当点K到达点N时,求出t的值; -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把P’(y1,x1)叫做点P的友好点,已知点
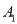 的友好点为
的友好点为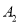 ,点
,点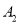 的友好点为
的友好点为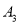 ,点
,点 的友好点为
的友好点为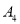 ,…,这样依次得到点.
,…,这样依次得到点.(1)当点
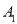 的坐标为(2,1),则点
的坐标为(2,1),则点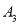 的坐标为___,点
的坐标为___,点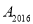 的坐标为___;
的坐标为___;(2)若
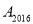 的坐标为(3,2),则设
的坐标为(3,2),则设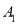 (x,y),求x+y的值;
(x,y),求x+y的值;(3)设点A1的坐标为(a,b),若
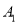 ,
,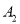 ,
,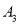 ,…
,…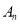 ,点
,点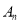 均在y轴左侧,求a、b的取值范围.
均在y轴左侧,求a、b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) (-4x2y)·(-x2y2)·(
 y)3; (2) (-3ab)(2a2b+ab-1) ;
y)3; (2) (-3ab)(2a2b+ab-1) ;(3) (m-
 )(m+
)(m+ ); (4) (-x-1)(-x+1) ; (5) ( - x - 5)2 ; (6)
); (4) (-x-1)(-x+1) ; (5) ( - x - 5)2 ; (6) ;
;(7)先化简,再求值:(x+1)2﹣(x+2)(x﹣2),其中
 ;
; (8)解方程组
 .
.
相关试题

