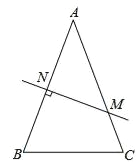
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
(1)若∠B=70°,则∠NMA的度数是 .
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
参考答案:
【答案】(1)50°;(2)①BC=6cm;②当点P与点M重合时,PB+CP的值最小,最小值是8cm.
【解析】试题分析:1)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;
(2)①根据垂直平分线的性质,可得AM与MB的关系,再根据三角形的周长,可得答案;
②根据两点之间线段最短,可得P点与M点的关系,可得PB+PC与AC的关系.
试题解析:(1)∵AB=AC,∴∠C=∠B=70°,∴∠A=180°-∠B-∠C=40°,
∵∠ANM=90°,∴∠NMA=90°-∠A= 50°,
故答案为:50°;
(2)如图:
①∵MN垂直平分AB.
∴MB=MA,
又∵△MBC的周长是14cm,
∴AC+BC=14cm,
∴BC=6cm;
②当点P与点M重合时,PB+CP的值最小,最小值是8cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师获得一张联欢晚会的门票,想奖给班级学校优秀的同学,通过考察,小明和小刚脱颖而出,但问题是只有一张门票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看晚会,他们各自提出了一个方案:
(1)小明的方案:将红桃2、3、4、5四张牌背面朝上,小明先抽一张,记下牌面数字后放回,小刚再从中抽一张,若两张牌上的数字之和是奇数,则小明看晚会,否则小刚看晚会,你认为小明的方案公平吗?请用列表法或画树状图的方法说明;
(2)小刚将小明的方案修改为只用红桃2、3、4三张牌,抽取方式规则不变,小刚的方案公平吗?(只回答,不说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足
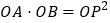 ,我们就把∠APB叫做∠MON的智慧角.
,我们就把∠APB叫做∠MON的智慧角.(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以点P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°. 求证:∠APB是∠MON的智慧角;
(2)如图3,C是函数
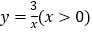 图象上的一个动点,过点C的直线CD分别交
图象上的一个动点,过点C的直线CD分别交 轴和
轴和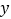 轴于点A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
轴于点A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC 与BD 交于O,AC=BD.
求证:(1)BC=AD;
(2)△OAB是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列数值中不是不等式5x≥2x+9的解的是( )
A.5
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各点在一次函数y=2x﹣3的图象上的是( )
A. ( 2,3) B. (2,1) C. (0,3) D. (3,0
-
科目: 来源: 题型:
查看答案和解析>>【题目】在函数y=2x中,y的值随x值的增大而_____.(填“增大”或“减小”)
相关试题

