【题目】如图,已知AC⊥BC,BD⊥AD,AC 与BD 交于O,AC=BD.
求证:(1)BC=AD;
(2)△OAB是等腰三角形.

参考答案:
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)根据AC⊥BC,BD⊥AD,得出△ABC与△BAD是直角三角形,再根据AC=BD,AB=BA,得出Rt△ABC≌Rt△BAD,即可证出BC=AD,
(2)根据Rt△ABC≌Rt△BAD,得出∠CAB=∠DBA,从而证出OA=OB,△OAB是等腰三角形.
【解答】证明:(1)∵AC⊥BC,BD⊥AD,
∴∠ADB=∠ACB=90°,
在Rt△ABC和Rt△BAD中,
∵![]() ,
,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD,
(2)∵Rt△ABC≌Rt△BAD,
∴∠CAB=∠DBA,
∴OA=OB,
∴△OAB是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=10,动点P从点A出发,以每秒1个单位的速度,沿线段AB向终点B运动,同时,另一个动点Q从点B出发,以每秒3个单位的速度在线段AB上来回运动(从点B向点A运动,到达点A后,立即原速返回,再次到达B点后立即调头向点A运动.) 当点P到达B点时,P,Q两点都停止运动.设点P的运动时间为x.
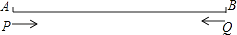
(1)当x=3时,线段PQ的长为 .
(2)当P,Q两点第一次重合时,求线段BQ的长.
(3)是否存在某一时刻,使点Q恰好落在线段AP的中点上?若存在,请求出所有满足条件的x的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B两点的坐标是A(5,a),B(b,4),若AB平行于x轴,且AB=3,则a+b的值为( )
A. ﹣1 B. 9 C. 12 D. 6或12
-
科目: 来源: 题型:
查看答案和解析>>【题目】把直线y=2x﹣1向上平移三个单位,则平移后直线与x轴的交点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a与b互为相反数,x与y互为倒数,则2014a﹣2015xy+2014b的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义a★b=a2﹣b,则(0★1)★2016= .
相关试题

