搜索
【题目】如图，
，
，
，…，
都是等腰直角三角形，其中点
，
，…，
在
轴上，点
，
，…，
在直线
上，已知
，则
的长为______________． 
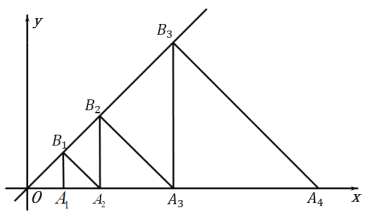
参考答案：
【答案】
【解析】
根据一次函数的性质可得∠B1OA1=45°，然后求出△OA2B2是等腰直角三角形，△OA3B2是等腰直角三角形，然后根据等腰直角三角形斜边上的高等于斜边的一半求出OA3，同理求出OA4，然后根据变化规律写出即可．
解：∵直线为y=x，
∴∠B1OA1=45°，
∵△A2B2A3，
∴B2A2⊥x轴，∠B2A3A2=45°，
∴△OA2B2是等腰直角三角形，△OA3B2是等腰直角三角形，
∴OA3=2A2B2=2OA2=2×2=4，
同理可求OA4=2OA3=2×4=23，
…，
所以，OA2020=22019．
故答案为：22019；
-
科目： 来源： 题型：
查看答案和解析>>【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的，如果规定向东为正，向西为负，他这天下午行驶里程如下：（单位：千米）
+15, -3, +14，-11，+10，-12，+4，-15，+16，-18
（1）他将最后一名乘客送到目的地时，距下午出车地点是多少千米？
（2）若汽车耗油量为
升∕千米，这天下午共耗油多少升 -
科目： 来源： 题型：
查看答案和解析>>【题目】某网店销售甲、乙两种羽毛球，已知甲种羽毛球每筒的售价比乙种羽毛球每筒的售价多15元，小彬从该网店购买了3筒甲种羽毛球和2筒乙种羽毛球，一共花费270元.
（1）该网店甲、乙两种羽毛球每筒的售价各是多少元？
（2）根据消费者需求，该网店决定购进甲、乙两种羽毛球各80筒.已知甲种羽毛球每筒的进价为50元，乙种羽毛球每筒的进价为40元.元旦期间该网店开展优惠促销活动，甲种羽毛球打折销售，乙种羽毛球售价不变，若所购进羽毛球均可全部售出，要使全部售出所购进的羽毛球的利润率是
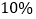，那么甲种羽毛球是按原销售价打几折销售的. -
科目： 来源： 题型：
查看答案和解析>>【题目】C点的坐标为（4，4），A为y轴负半轴上一动点，连CA，CB⊥CA交x轴于B．
（1）求OB﹣OA的值；
（2）E在x轴正半轴上，D在y轴负半轴上，∠DCE＝45°，转动∠DCE，求线段BE、DE和AD之间的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知A(0,a)、B(b, 0)，且a、b满足：
，点D为x正半轴上一动点 (1)求A、B两点的坐标
(2)如图，∠ADO的平分线交y轴于点C，点 F为线段OD上一动点，过点F作CD的平行线交y轴于点H，且∠AFH=45°， 判断线段AH、FD、AD三者的数量关系，并予以证明
(3)以AO为腰，A为顶角顶点作等腰△ADO，若∠DBA=30°，直接写出∠DAO的度数
-
科目： 来源： 题型：
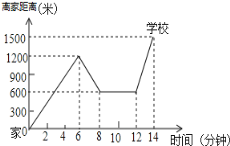
查看答案和解析>>【题目】“珍重生命，注意安全！”同学们在上下学途中一定要注意骑车安全．小明骑单车上学，当他骑了一段时，想起要买某本书，于是又折回到刚经过的新华书店，买到书后继续去学校，以下是他本次所用的时间与路程的关系示意图．根据图中提供的信息回答下列问题：
（1）小明家到学校的路程是多少米；
（2）小明在书店停留了多少分钟；
（3）本次上学途中，小明一共行驶了多少米？一共用了多少分钟？
-
科目： 来源： 题型：
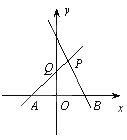
查看答案和解析>>【题目】如图，直线PA是一次函数y=x+1的图象，直线PB是一次函数y=-2x+2的图象.
（1）求A、B、P三点的坐标；
（2）求四边形PQOB的面积；
相关试题
