【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(1,﹣4),B(5,﹣4),C(4,﹣1).
(1)将△ABC经过平移得到△A1B1C1,若点C的应点C1的坐标为(2,5),写出点A,B的对应点A1,B1的坐标;
(2)在如图的坐标系中画出△A1B1C1,并画出与△A1B1C1关于原点O成中心对称的△A2B2C2.
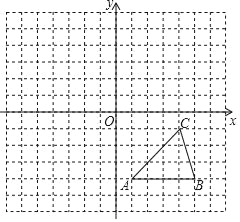
参考答案:
【答案】(1)A1,B1的坐标分别为(﹣1,2),(3,2),(2)如图所示:△A1B1C1;△A2B2C2即为所求.见解析.
【解析】
(1)根据平移的性质画出图形,进而得出坐标即可;(2)根据平移的性质和关于原点O成中心对称的性质画出图形即可.
(1)如图所示:
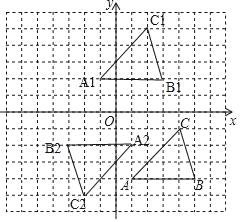
A1,B1的坐标分别为(﹣1,2),(3,2),
故答案为:(﹣1,2),(3,2),
(2)如图所示:△A1B1C1;△A2B2C2即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:a*b=10a×10b,例如图3*4=103×104=107.
(1)试求12*3和2*5的值;
(2)想一想(a*b)*c与a*(b*c)相等吗?如果相等,请验证你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为24的等边三角形,△CDE是等腰三角形,其中DC=DE=10,∠CDE=120°,点E在BC边上,点F是BE的中点,连接AD、DF、AF,则AF的长为_____.

-
科目: 来源: 题型:
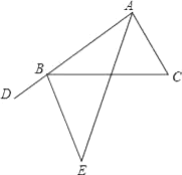
查看答案和解析>>【题目】完成下面证明:如图,B是射线AD上一点,∠DAE=∠CAE,∠DAC=∠C=∠CBE
(1)求证:∠DBE=∠CBE
证明:∵∠C=∠CBE(已知)
∴BE∥AC________
∴∠DBE=∠DAC________
∵∠DAC=∠C(已知)
∴∠DBE=∠CBE________
(2)请模仿(1)的证明过程,尝试说明∠E=∠BAE.
-
科目: 来源: 题型:
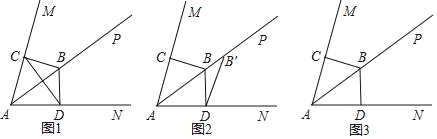
查看答案和解析>>【题目】如图1,已知射线AP是∠MAN的角平分线,点B为射线AP上的一点且AB=10,过点B分别作BC⊥AM于点C,作BD⊥AN于点D,BC=6.
(1)在图1中连接CD交AB于点O.求证:AB垂直平分CD;
(2)从A,B两题中任选一题作答,我选择 题
A.将图1中的△ABC沿射线AP的方向平移得到△ABC,点A、B、C的对应点分别为A′、B′、C′.若平移后点B的对应点B′的位置如图2,连接DB′.
①请在图2中画出此时的△A′B′C′,并在图中标注相应的字母;
②若图2中的DB′∥A′C′,写出平移的距离.
B.将图1中的△ABC沿射线AP的方向平移得到△A′B′C′,点A、B、C的对应点分别为A′、B′、C′.
①在△A′B′C′平移的过程中,若点C′与点D的连线恰好经过点B,请在图3中画出此时的△A′B′C′,并在图中标注相应的字母;
②如图3,点C′与点D的连线恰好经过点B,写出此时平移的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
问题情境:如图1,在△ABC中,AB=AC,点D,E分别是边AB,AC上的点,且AD=AE,连接DE,易知BD=CE.将△ADE绕点A顺时针旋转角度α(0°<α<360°),连接BD,CE,得到图2.
(1)变式探究:如图2,若0°<α<90°,则BD=CE的结论还成立吗?若成立,请证明;若不成立,请说明理由;
(2)拓展延伸:若图1中的∠BAC=120°,其余条件不变,请解答下列问题:
从A,B两题中任选一题作答我选择 题
A.①在图1中,若AB=10,求BC的长;
②如图3,在△ADE绕点A顺时针旋转的过程中,当DE的延长线经过点C时,请直接写出线段AD,BD,CD之间的等量关系;
B.①在图1中,试探究BC与AB的数量关系,并说明理由;
②在△ADE绕点A顺时针旋转的过程中,当点D,E,C三点在同一条直线上时,请借助备用图探究线段AD,BD,CD之间的等量关系,并直接写出结果.

-
科目: 来源: 题型:
查看答案和解析>>【题目】新定义:若∠α的度数是∠β的度数的n倍,则∠α叫做∠β的n倍角.
(1)若∠M=10°21′,请直接写出∠M的3倍角的度数;
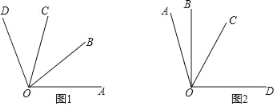
(2)如图1,若∠AOB=∠BOC=∠COD,请直接写出图中∠AOB的所有2倍角;
(3)如图2,若∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,且∠BOD=90°,求∠BOC的度数.
相关试题

