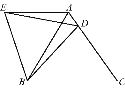
【题目】在等边△ABC中,D是AC边上一点,连接BD,将△BCD绕点B逆时针旋转60°得到△BAE,连接ED,若BC=5,BD=4,有下列结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△ADE的周长是9.其中正确的个数是( )
A. 4 B. 3 C. 2 D. 1
参考答案:
【答案】B
【解析】
首先由旋转的性质可知∠EAB=∠ABC=60°,所以可得AE∥BC;由△ABC是等边三角形得出AC=AB=BC=5,根据图形旋转的性质得出AE=CD,BD=BE,故可得出AE+AD=AD+CD=AC=5,由∠EBD=60°,BE=BD即可判断出△BDE是等边三角形,故DE=BD=4,故△AED的周长=AE+AD+DE=AC+BD=9,综上可得答案.
∵△ABC是等边三角形,
∴∠ABC=∠C=60°,
∵将△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠EAB=∠C=∠ABC=60°,
∴AE∥BC,故结论①正确;
∵没有条件证明∠ADE=∠BDC,
∴结论②错误,
∵△ABC是等边三角形,
∴AC=AB=BC=5,
∵△BAE是△BCD逆时针旋转60°得出,
∴AE=CD,BD=BE,∠EBD=60°,
∴AE+AD=AD+CD=AC=5,
∵∠EBD=60°,BE=BD,
∴△BDE是等边三角形,故结论③正确;
∴DE=BD=4,
∴△AED的周长=AE+AD+DE=AC+BD=9,故结论④正确;
综上所述:①③④结论正确,共3个,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=6,AD=10,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】填写推理理由:
已知:如图,D,F,E分别是BC,AC,AB上的点,DF∥AB,DE∥AC,

试说明∠EDF=∠A.
解:∵DF∥AB(已知),
∴∠A+∠AFD=180°(____________________).
∵DE∥AC(已知),
∴∠AFD+∠EDF=180°(____________________).
∴∠A=∠EDF(____________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为
 cm,AC=8cm,设运动时间为t秒.
cm,AC=8cm,设运动时间为t秒. 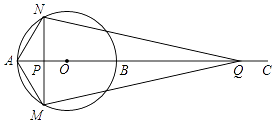
(1)求证:NQ=MQ;
(2)填空: ①当t=时,四边形AMQN为菱形;
②当t=时,NQ与⊙O相切. -
科目: 来源: 题型:
查看答案和解析>>【题目】为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
社团类别
人数
占总人数比例
球类
60
m
舞蹈
30
0.25
健美操
n
0.15
武术
12
0.1

(1)求样本容量及表格中m、n的值;
(2)请补全统计图;
(3)被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3000名学生,请估计该校最喜欢足球的人数. -
科目: 来源: 题型:
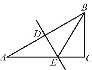
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=60°,AB的垂直平分线分别交AB,AC于点D和点E.若CE=2,则AB的长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】读句画图:如图,直线CD与直线AB相交于C,
根据下列语句画图:

(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.
相关试题

