【题目】如图,直线y=kx+b与双曲线y=![]() 相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=
相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=![]() ,CE=2,点A的横坐标是1.
,CE=2,点A的横坐标是1.
(1)求点A,G的坐标;
(2)求直线AB的解析式.

参考答案:
【答案】(1)(2,![]() )(2)y=
)(2)y=![]() x+
x+![]() .
.
【解析】
试题分析:(1)由矩形的性质结合DE=![]() ,可知点G的纵坐标为
,可知点G的纵坐标为![]() ,分别令双曲线y=
,分别令双曲线y=![]() 中x=1、y=
中x=1、y=![]() ,即可求出点A、G的坐标;
,即可求出点A、G的坐标;
(2)分别令直线y=kx+b中y=0、y=![]() ,求出点C、E的横坐标,结合线段CE=2即可得出关于k的一元一次方程,解方程即可得出k值,将k值和点A的坐标代入到直线y=kx+b中得出关于b的一元一次方程,解方程即可得出结论.
,求出点C、E的横坐标,结合线段CE=2即可得出关于k的一元一次方程,解方程即可得出k值,将k值和点A的坐标代入到直线y=kx+b中得出关于b的一元一次方程,解方程即可得出结论.
试题解析:(1)∵DE=![]() ,且四边形DEFG为矩形,
,且四边形DEFG为矩形,
∴GF=DE=![]() .
.
令双曲线y=![]() 中x=1,则y=
中x=1,则y=![]() =3,
=3,
∴点A的坐标为(1,3);
令双曲线y=![]() 中y=
中y=![]() ,则
,则![]() =
=![]() ,解得:x=2,
,解得:x=2,
∴点G的坐标为(2,![]() ).
).
(2)令直线y=kx+b中y=![]() ,则
,则![]() =kx+b,解得:x=
=kx+b,解得:x=![]() ,
,
即点D的坐标为(![]() ,
,![]() ),点E的坐标为(
),点E的坐标为(![]() ,0);
,0);
令直线y=kx+b中y=0,则0=kx+b,解得:x=﹣![]() ,
,
即点C的坐标为(﹣![]() ,0).
,0).
∵CE=![]() ﹣(﹣
﹣(﹣![]() )=2,
)=2,
∴![]() =2k,解得:k=
=2k,解得:k=![]() ,
,
∴直线AB的解析式为y=![]() x+b,
x+b,
∵点A(1,3)在直线AB上,
∴3=![]() +b,解得:b=
+b,解得:b=![]() ,
,
∴直线AB的解析式为y=![]() x+
x+![]() .
.
-
科目: 来源: 题型:
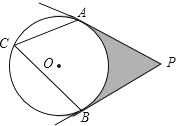
查看答案和解析>>【题目】如图,PA,PB分别与⊙O相切于A,B两点,∠ACB=60°.
(1)求∠P的度数;
(2)若⊙O的半径长为4cm,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=ax+b(a<0)的图象与x的交点坐标是(3,0),那么关于x的方程ax+b=0的解是 ______,关于x的不等式ax+b>0的解集是_______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且mn≠0),在同一平面立角坐标系的图象是( )
A.
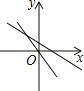 B.
B.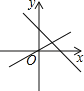 C.
C.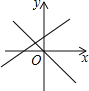 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】a是方程x2+x﹣1=0的一个根,则代数式﹣2a2﹣2a+2020的值是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在一次函数y=kx+3中,函数值y随x的增大而增大,请你写出一个符合条件的k的值:_______.
(2)已知一个函数,当x>0时,函数值y随x的增大而减小,请你写出符合条件的一个函数表达式:_________.
(3)若一次函数y=kx+b的图象经过点(0,-2)和(-2,0),则y随x的增大而_______.
(4)若点(-1,y1),(2,y2)是直线y=2x+1上的两点,则y1___y2(填“>”“<”或“=”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)小慧和小聪沿图1中的景区公路游览.小慧乘坐车速为30km/h的电动汽车,早上7:00从宾馆出发,游玩后中午12:00回到宾馆.小聪骑车从飞瀑出发前往宾馆,速度为20km/h,途中遇见小慧时,小慧恰好游完一景点后乘车前往下一景点.上午10:00小聪到达宾馆.图2中的图象分别表示两人离宾馆的路程s(km)与时间t(h)的函数关系.试结合图中信息回答:

(1)小聪上午几点钟从飞瀑出发?
(2)试求线段AB、GH的交点B的坐标,并说明它的实际意义.
(3)如果小聪到达宾馆后,立即以30km/h的速度按原路返回,那么返回途中他几点钟遇见小慧?
相关试题

