【题目】一次函数y=mx+n与正比例函数y=mnx(m,n是常数,且mn≠0),在同一平面立角坐标系的图象是( )
A.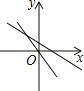 B.
B.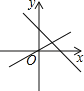 C.
C.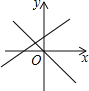 D.
D.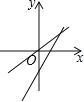
参考答案:
【答案】A
【解析】
试题分析:根据一次函数与正比例函数的性质对四个选项进行逐一分析即可.
解:A、由一次函数的图象可知,m<0,n>0,故mn<0;由正比例函数的图象可知mn<0,两结论一致,故本选项正确;
B、由一次函数的图象可知,m<0,n>0,故mn<0;由正比例函数的图象可知mn>0,两结论不一致,故本选项不正确;
C、由一次函数的图象可知,m>0,n>0,故mn>0;由正比例函数的图象可知mn<0,两结论不一致,故本选项不正确;
D、由一次函数的图象可知,m>0,n<0,故n>0,mn<0;由正比例函数的图象可知mn>0,两结论不一致,故本选项不正确.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M,B,C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y.
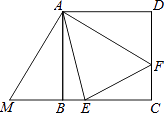
(1)图中△ADF可以绕点按顺时针方向旋转°后能与△重合;
(2)用x、y的代数式表示△AEM与△EFC的面积. -
科目: 来源: 题型:
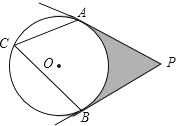
查看答案和解析>>【题目】如图,PA,PB分别与⊙O相切于A,B两点,∠ACB=60°.
(1)求∠P的度数;
(2)若⊙O的半径长为4cm,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=ax+b(a<0)的图象与x的交点坐标是(3,0),那么关于x的方程ax+b=0的解是 ______,关于x的不等式ax+b>0的解集是_______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b与双曲线y=
 相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=
相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE= ,CE=2,点A的横坐标是1.
,CE=2,点A的横坐标是1.(1)求点A,G的坐标;
(2)求直线AB的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】a是方程x2+x﹣1=0的一个根,则代数式﹣2a2﹣2a+2020的值是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在一次函数y=kx+3中,函数值y随x的增大而增大,请你写出一个符合条件的k的值:_______.
(2)已知一个函数,当x>0时,函数值y随x的增大而减小,请你写出符合条件的一个函数表达式:_________.
(3)若一次函数y=kx+b的图象经过点(0,-2)和(-2,0),则y随x的增大而_______.
(4)若点(-1,y1),(2,y2)是直线y=2x+1上的两点,则y1___y2(填“>”“<”或“=”).
相关试题

