Question

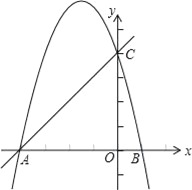
【题目】如图，抛物线y=ax2﹣bx﹣4a交x轴于点A、B，交y轴于点C，其中点B、C的坐标分别为B（1，0）、C（0，4）．

（1）求抛物线的解析式，并用配方法把其化为y=a（x﹣h）2+k的形式，写出顶点坐标；

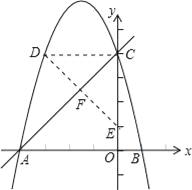
（2）已知点D（m，1﹣m）在第二象限的抛物线上，求出m的值，并直接写出点D关于直线AC的对称点E的坐标．

Answer 1

【答案】（1）此抛物线的解析式为y=﹣x2﹣3x+4． ；（-， ）；（2）m1=﹣3，m2=1．E（0，1）．

【解析】试题分析：（1）由抛物线y=ax2+bx﹣4a经过A（1，0）、C（0，4）两点，利用待定系数法即可求得抛物线的解析式；

（2）由点D（m，1﹣m）在抛物线y=﹣x2﹣3x+4上，即可求得点D的坐标，则可求得∠CBO的度数，然后过点D作DF⊥BC于F，延长DE交y轴于E，又由点E即为点D关于直线BC的对称点，即可求得点E的坐标．

试题解析：（1）抛物线y=ax2+bx﹣4a经过A（1，0）、C（0，4）两点，

∴，

解得．

∴此抛物线的解析式为y=﹣x2﹣3x+4．

（2）∵点D（m，1﹣m）在抛物线y=﹣x2﹣3x+4上，

∴﹣m2﹣3m+4=1﹣m，

解得m1=﹣3，m2=1．

∵点D在第二象限，

∴D（﹣3，4）．

令y=﹣x2﹣3x+4=0，

解得x1=1，x2=﹣4．

∴B（﹣4，0）．

∴∠CBO=45°．

连接DC，

易知DC∥BA，DC⊥CO，DC=3．

∴∠DCA=∠CAO=45°．

∴∠ACD=45°．

过点D作DF⊥BC于F，延长DE交y轴于E，

∴∠D=45°．

∴∠CFE=45°．

∴DF=CF=EF．

∴点E即为点D关于直线BC的对称点．

∴CD=CE=3，

∴OE=1

∴E（0，1）．