【题目】已知抛物线y=![]() x2+(m﹣2)x+2m﹣6的对称轴为直线x=1,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
x2+(m﹣2)x+2m﹣6的对称轴为直线x=1,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
(1)求m的值;
(2)直线l经过B、C两点,求直线l的解析式.
参考答案:
【答案】(1)m=1;(2)y=﹣x﹣4.
【解析】试题分析:(1)由对称轴公式即可求出m的值;(2)由抛物线的解析式求出A、B、C的坐标,由待定系数法求出直线l的解析式即可.
试题解析:(1)∵抛物线y=![]() x2+(m﹣2)x+2m﹣6的对称轴为直线x=1,
x2+(m﹣2)x+2m﹣6的对称轴为直线x=1,
∴﹣![]() =1,
=1,
解得:m=1;
(2)∵m=1,
∴抛物线的解析式为y=![]() x2﹣x﹣4,
x2﹣x﹣4,
当y=0时, ![]() x2﹣x﹣4=0,
x2﹣x﹣4=0,
解得:x=﹣2或x=4,
∴A(﹣2,0),B(4,0),
当x=0时,y=﹣4,
∴C(0,﹣4),
设直线l的解析式为y=kx+b,
根据题意得: ![]() ,
,
解得: ![]() ,
,
∴直线l的解析式为y=﹣x﹣4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用不等式的基本性质求下列不等式的解集,并写出变形的依据.
(1)若x+2016>2017,则x___________;
(______________________)
(2)若2x>-
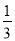 ,则x____________;
,则x____________;(__________________________)
(3)若-2x>-
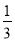 ,则x____________;
,则x____________;(___________________________)
(4)若-
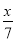 >-1,则x_________.
>-1,则x_________.(_______________________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=﹣x2的图象上有三个点:A(﹣3,y1),B(﹣1,y2),C(2,y3),则y1,y2,y3的大小关系为( )
A.y1>y2>y3B.y2>y3>y1C.y3>y2>y1D.y3>y1>y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】指出下列各式成立的条件:
(1)由mx<n,得x<
 ;
;(2)由a<b,得ma>mb;
(3)由a>-5,得a2≤-5a;
(4)由3x>4y,得3x-m>4y-m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣8(x+m)2+n的图象的顶点坐标是(﹣5,﹣4),那么一次函数y=mx+n的图象经过第_____象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用不等式的性质解下列不等式.
(1)8-3x<4-x;
(2)2(x-1)<3(x+1)-2.
(3)
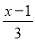 ≥
≥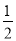 x-1.
x-1. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(
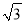 ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: 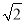 =1.41,
=1.41,  =1.73)
=1.73)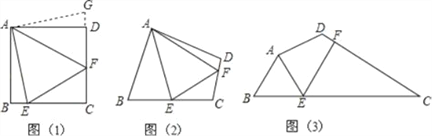
相关试题

