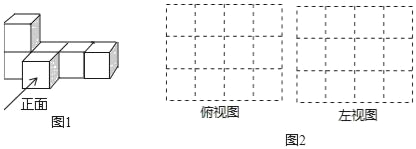
【题目】(1)如图1是由大小相同的小立方块搭成的几何体,请在图2的方格中画出从上面和左面看到的该几何体的形状图.(只需用2B铅笔将虚线化为实线)
(2)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最多需要 个小立方块.
参考答案:
【答案】(1)详见解析;(2)9
【解析】
(1)从上面看得到从左往右4列正方形的个数依次为1,2,1,1,依此画出图形即可;从左面看得到从左往右2列正方形的个数依次为2,1;依此画出图形即可;
(2)由俯视图易得最底层小立方块的个数,由左视图找到其余层数里最多个数相加即可.
解:(1)如图所示:
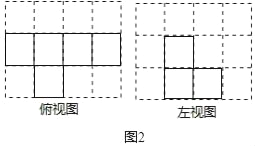
(2)搭这样的一个几何体最大需要5+4=9个小立方块.
故答案为:9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.
(1)求降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?
-
科目: 来源: 题型:
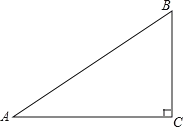
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′E⊥AC时,A′B=_________.
-
科目: 来源: 题型:
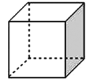
查看答案和解析>>【题目】用一个平面去截正方体(如图),下列关于截面(截出的面)形状的结论:
①可能是锐角三角形;②可能是钝角三角形;
③可能是长方形;④可能是梯形.
其中正确结论的是______(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角板的直角顶点放在点O处(∠DOE=90°).
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O转动,若OD恰好平分∠BOC,求∠AOE的度数。
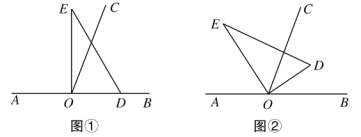
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校积极开展“阳光体育进校园”活动,决定开设 A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目,规定每个学生必须参加一项活动。学校为了了解学生最喜欢哪一种运动项目,设计了以下四种调查方案.
方案一:调查该校七年级女生喜欢的运动项目
方案二:调查该校每个班级学号为 5 的倍数的学生喜欢的运动项目
方案三:调查该校书法小组的学生喜欢的运动项目
方案四:调查该校田径队的学生喜欢的运动项目
(1)上面的调查方案最合适的是 ;
学校体育组采用了(1)中的方案,将调查的结果绘制成如下两幅不完整的统计图表.
最喜欢的运动项目人数调查统计表 最喜欢的运动项目人数分布统计图


请你结合图表中的信息解答下列问题:
(2)这次抽样调查的总人数是 ,m= ;
(3)在扇形统计图中,A 项目对应的圆心角的度数为 ;
(4)已知该校有 1200 名学生,请根据调查结果估计全校学生最喜欢乒乓球的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有a枚棋子,按图1的方式摆放时刚好围成m个小正方形,按图2的方式摆放刚好围成2n个小正方形。
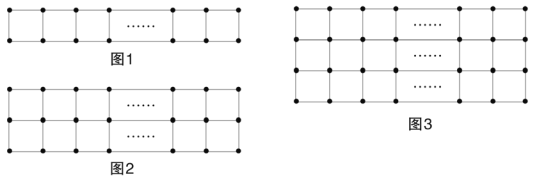
(1)用含m的代数式表示a,有a= ;用含n的代数式表示a,有a= ;
(2)若这a枚棋子按图3的方式摆放恰好围成3p个小正方形,
①P的值能取7吗?请说明理由;
②直接写出a的最小值:
相关试题

