【题目】在平面直角坐标系xOy中,抛物线y=x2+mx+n﹣1的对称轴为x=2. 
(1)m的值为;
(2)若抛物线与y轴正半轴交于点A,其对称轴与x轴交于点B,当△OAB是等腰直角三角形时,求n的值;
(3)点C的坐标为(3,0),若该抛物线与线段OC有且只有一个交点,求n的取值范围.
参考答案:
【答案】
(1)-4
(2)解:把m=﹣4代入抛物线y=x2+mx+n﹣1得:
y=x2﹣4x+n﹣1,
当x=0时,y=n﹣1,
∴A(0,n﹣1),B(2,0),
∵△OAB是等腰直角三角形,
∴OA=OB,
即:n﹣1=2,n=3
(3)解:①如图1,当抛物线顶点在x轴上时,
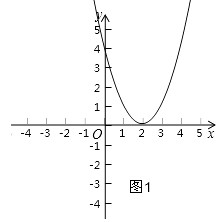
△=0,(﹣4)2﹣4×1×(n﹣1)=0
n=5,
②如图2,当抛物线过点C(3,0)时,

把(3,0)代入得:32﹣4×3+n﹣1=0,
n=4,
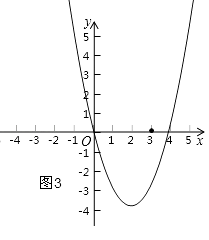
③如图3,当抛物线过原点时,n﹣1=0,n=1,
结合图象可得,1≤n<4或n=5.
【解析】解:(1)对称轴:x=﹣ ![]() =2,m=﹣4;
=2,m=﹣4;
【考点精析】本题主要考查了等腰直角三角形和抛物线与坐标轴的交点的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】表是二次函数y=ax2+bx+c的部分x,y的对应值:
x
…
﹣1
﹣

0

1

2

3
…
y
…
m

﹣1

﹣2

﹣1

2
…
(1)二次函数图象的开口向 , 顶点坐标是 , m的值为;
(2)当x>0时,y的取值范围是;
(3)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O分别交AC,BC于点D,E,过点A作⊙O的切线交BC的延长线于点F,连接AE.

(1)求证:∠ABC=2∠CAF;
(2)过点C作CM⊥AF于M点,若CM=4,BE=6,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小华在研究函数y1=x与y2=2x图象关系时发现:如图所示,当x=1时,y1=1,y2=2;当x=2时,y1=2,y2=4;…;当x=a时,y1=a,y2=2a.他得出如果将函数y1=x图象上各点的横坐标不变,纵坐标变为原来的2倍,就可以得到函数y2=2x的图象.类比小华的研究方法,解决下列问题:

(1)如果函数y=3x图象上各点横坐标不变,纵坐标变为原来的3倍,得到的函数图象的表达式为;
(2)①将函数y=x2图象上各点的横坐标不变,纵坐标变为原来的倍,得到函数y=4x2的图象; ②将函数y=x2图象上各点的纵坐标不变,横坐标变为原来的2倍,得到图象的函数表达式为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,∠BAD=α,E为对角线AC上的一点(不与A,C重合),将射线EB绕点E顺时针旋转β角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.小宇发现点E的位置,α和β的大小都不确定,于是他从特殊情况开始进行探究.

(1)如图1,当α=β=90°时,菱形ABCD是正方形.小宇发现,在正方形中,AC平分∠BAD,作EM⊥AD于M,EN⊥AB于N.由角平分线的性质可知EM=EN,进而可得△EMF≌△ENB,并由全等三角形的性质得到EB与EF的数量关系为 .
(2)如图2,当α=60°,β=120°时,
①依题意补全图形;
②请帮小宇继续探究(1)的结论是否成立.若成立,请给出证明;若不成立,
请举出反例说明;
(3)小宇在利用特殊图形得到了一些结论之后,在此基础上对一般的图形进行了探究,设∠ABE=γ,若旋转后所得的线段EF与EB的数量关系满足(1)中的结论,请直接写出角α,β,γ满足的关系: -
科目: 来源: 题型:
查看答案和解析>>【题目】点P到∠AOB的距离定义如下:点Q为∠AOB的两边上的动点,当PQ最小时,我们称此时PQ的长度为点P到∠AOB的距离,记为d(P,∠AOB).特别的,当点P在∠AOB的边上时,d(P,∠AOB)=0.在平面直角坐标系xOy中,A(4,0).

(1)如图1,若M(0,2),N(﹣1,0),则d(M,∠AOB)= , d(N,∠AOB)=;
(2)在正方形OABC中,点B(4,4).如图2,若点P在直线y=3x+4上,且d(P,∠AOB)=2 ,求点P的坐标;
,求点P的坐标;
(3)如图3,若点P在抛物线y=x2﹣4上,满足d(P,∠AOB)=2 的点P有个,请你画出示意图,并标出点P.
的点P有个,请你画出示意图,并标出点P. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′是直线y=
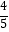 x上一点,则点B与其对应点B′间的距离为 .
x上一点,则点B与其对应点B′间的距离为 . 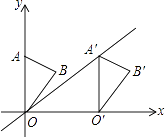
相关试题

