Question

【题目】表是二次函数y=ax2+bx+c的部分x，y的对应值：

x	…	﹣1	﹣	0		1		2		3	…
y	…	m		﹣1		﹣2		﹣1		2	…

（1）二次函数图象的开口向 ， 顶点坐标是 ， m的值为；
（2）当x＞0时，y的取值范围是；
（3）当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时，n的取值范围是 ．

Answer 1

【答案】
（1）上；（1，﹣2）；2
（2）y≥﹣2
（3）n＞﹣3
【解析】解：（1）把点（0，﹣1），（1，﹣2）和（2，﹣1）代入二次函数解析式可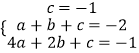得 ，解得 ，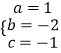
∴二次函数解析式为y=x2﹣2x﹣1=（x﹣1）2﹣2，
∴二次函数图象开口向上，顶点坐标为（1，﹣2），
令x=﹣1，代入可得m=2，
所以答案是：上；（1，﹣2）；2；
2）∵y=（x﹣1）2﹣2，
∴当x=1时，y有最小值﹣2，
∴当x＞0时，y≥﹣2，
所以答案是：y≥﹣2；
3）在y=x+n中，令x=1代入可得y=1+n，
∵抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时，
∴1+n＞﹣2，解得n＞﹣3，
所以答案是：n＞﹣3．
【考点精析】关于本题考查的一次函数的性质和二次函数的性质，需要了解一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．