Question

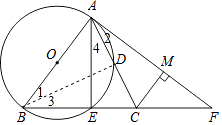
【题目】如图，在△ABC中，AB=BC，以AB为直径的⊙O分别交AC，BC于点D，E，过点A作⊙O的切线交BC的延长线于点F，连接AE．
（1）求证：∠ABC=2∠CAF；
（2）过点C作CM⊥AF于M点，若CM=4，BE=6，求AE的长．

Answer 1

【答案】
（1）证明：连接BD，

∵AB是直径，

∴∠ADB=90°，

∵AF是⊙O的切线，

∴∠BAF=90°．

∴∠1+∠BAC=∠2+∠BAC=90°．

∴∠1=∠2．

∵AB=BC，

∴∠ABC=2∠1=2∠2

（2）解：∵∠1=∠2=∠3，∠3=∠4，

∴∠2=∠4．

∵AB是直径，

∴CE⊥AE，

∵CM⊥AF，CM=4，

∴CE=CM=4，

∵BE=6，

∴AB=BC=BE+EC=10．

在Rt△ABE中，

【解析】（1）首先连接BD，由AB为直径，可得∠ADB=90°，然后由等角的余角相等，证得∠1=∠2，继而证得结论；（2）由圆周角定理，易证得∠2=∠4，又由AB为直径，CM⊥AF，可求得CE=CM=4，继而求得AB的长，则可求得答案．
【考点精析】关于本题考查的切线的性质定理，需要了解切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案．