搜索
【题目】如图，在平面直角坐标系中，点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点A′是直线y= 
x上一点，则点B与其对应点B′间的距离为 ．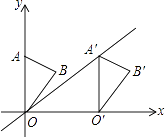 
参考答案：
【答案】5
【解析】解：如图，连接AA′、BB′．
∵点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O′A′B′，
∴点A′的纵坐标是4．
又∵点A的对应点在直线y= 
x上一点，
∴4= x，解得x=5．
∴点A′的坐标是（5，4），
∴AA′=5．
∴根据平移的性质知BB′=AA′=5．
故答案为：5．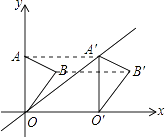
根据平移的性质知BB′=AA′．由一次函数图象上点的坐标特征可以求得点A′的坐标，所以根据两点间的距离公式可以求得线段AA′的长度，即BB′的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，抛物线y=x2+mx+n﹣1的对称轴为x=2．
（1）m的值为；
（2）若抛物线与y轴正半轴交于点A，其对称轴与x轴交于点B，当△OAB是等腰直角三角形时，求n的值；
（3）点C的坐标为（3，0），若该抛物线与线段OC有且只有一个交点，求n的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】在菱形ABCD中，∠BAD=α，E为对角线AC上的一点（不与A，C重合），将射线EB绕点E顺时针旋转β角之后，所得射线与直线AD交于F点．试探究线段EB与EF的数量关系．小宇发现点E的位置，α和β的大小都不确定，于是他从特殊情况开始进行探究．
（1）如图1，当α=β=90°时，菱形ABCD是正方形．小宇发现，在正方形中，AC平分∠BAD，作EM⊥AD于M，EN⊥AB于N．由角平分线的性质可知EM=EN，进而可得△EMF≌△ENB，并由全等三角形的性质得到EB与EF的数量关系为 ．
（2）如图2，当α=60°，β=120°时，
①依题意补全图形；
②请帮小宇继续探究（1）的结论是否成立．若成立，请给出证明；若不成立，
请举出反例说明；
（3）小宇在利用特殊图形得到了一些结论之后，在此基础上对一般的图形进行了探究，设∠ABE=γ，若旋转后所得的线段EF与EB的数量关系满足（1）中的结论，请直接写出角α，β，γ满足的关系： -
科目： 来源： 题型：
查看答案和解析>>【题目】点P到∠AOB的距离定义如下：点Q为∠AOB的两边上的动点，当PQ最小时，我们称此时PQ的长度为点P到∠AOB的距离，记为d（P，∠AOB）．特别的，当点P在∠AOB的边上时，d（P，∠AOB）=0．在平面直角坐标系xOy中，A（4，0）．
（1）如图1，若M（0，2），N（﹣1，0），则d（M，∠AOB）= ， d（N，∠AOB）=；
（2）在正方形OABC中，点B（4，4）．如图2，若点P在直线y=3x+4上，且d（P，∠AOB）=2
，求点P的坐标；
（3）如图3，若点P在抛物线y=x2﹣4上，满足d（P，∠AOB）=2 的点P有个，请你画出示意图，并标出点P． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某抛物线的对称轴为直线x=2，点E是该抛物线顶点，抛物线与y轴交于点C，过点C作CD∥x轴，与抛物线交于点B，与对称轴交于点D，点A是对称轴上一点，连结AC、AB，若△ABC是等边三角形，则图中阴影部分图形的面积之和是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个不透明的盒子里装有三个分别写有数字6，﹣2，7的小球，它们的形状、大小、质地完全相同，先从盒子里随机抽取一个小球，记下数字后放回盒子，摇匀后再随机取出一个小球，记下数字，请你用画树状图或列表的方法求两次取出小球上的数字和大于10的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“今天你光盘了吗？”这是国家倡导“厉行节约，反对浪费”以来的时尚流行语．某校团委随机抽取了部分学生，对他们进行了关于“光盘行动”所持态度的调查，并根据调查收集的数据绘制了如下两幅不完整的统计图：
根据上述信息，解答下列问题：
（1）抽取的学生人数为；
（2）将两幅统计图补充完整；
（3）请你估计该校1200名学生中对“光盘行动”持赞成态度的人数．
相关试题
