【题目】如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标分别是( )

A. (2,2),(3,4),(1,7) B. (2,2),(4,3),(1,7)
C. (-2,2),(3,4),(1,7) D. (2,-2),(4,3),(1,7)
参考答案:
【答案】C
【解析】
直接利用平移中点的变化规律:
①向右平移a个单位,坐标P(x,y)P(x+a,y);
②向左平移a个单位,坐标P(x,y)P(x-a,y);
③向上平移b个单位,坐标P(x,y)P(x,y+b);
④向下平移b个单位,坐标P(x,y)P(x,y-b);
将图中的三个点的坐标,根据上面的规律,横坐标加2,纵坐标加3,即可得到平移后的坐标.
由题意可知此题平移规律是:(x+2,y+3),
照此规律计算可知原三个顶点(-4,-1),(1,1),(-1,4),平移后三个顶点的坐标是(-2,2),(3,4),(1,7).
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.

(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PCPA;
(3)当AC=6,CP=3时,求sin∠PAB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD的边长为6cm,点E、M分别是线段BD、AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图1,若点M与点D重合,求证:AF=MN;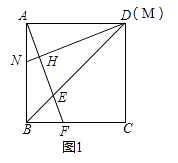
(2)如图2,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以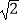 cm/s的速度沿BD向点D运动,运动时间为t s.
cm/s的速度沿BD向点D运动,运动时间为t s.
①设BF=y cm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度,已知动点A、B的速度比为1:3(速度单位:1个单位长度秒).

(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,满足OB=2OA?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(3,2).点D、E分别在AB、BC边上,BD=BE=1.沿直线DE将△BDE翻折,点B落在点B′处.则点B′的坐标为_____.
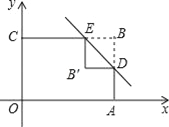
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC?若存在这样一点,求出点Q的坐标;若不存在,试说明理由.
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),给出下列结论:①
 的值不变,②
的值不变,② 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).

(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
相关试题

