【题目】正方形ABCD的边长为6cm,点E、M分别是线段BD、AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图1,若点M与点D重合,求证:AF=MN;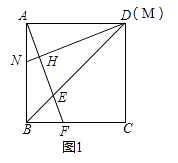
(2)如图2,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以 ![]() cm/s的速度沿BD向点D运动,运动时间为t s.
cm/s的速度沿BD向点D运动,运动时间为t s.
①设BF=y cm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.
参考答案:
【答案】
(1)
解:∵四边形ABCD 是正方形,
∴AD=AB,∠BAD=90°,
∵MN⊥AF,
∴∠AHM=90°,
∴∠BAF+∠MAH=∠MAH+∠AMH=90°,
∴∠BAF=∠AMH,
在△AMN与△ABF中,  ,
,
∴△AMN≌△ABF,
∴AF=MN
(2)
解:①∵AB=AD=6,
∴BD=6 ![]() ,
,
由题意得,DM=t,BE= ![]() t,
t,
∴AM=6﹣t,DE=6 ![]() ﹣
﹣ ![]() t,
t,
∵AD∥BC,
∴△ADE∽△FBE,
∴ ![]() ,即
,即 ![]() ,
,
∴y= ![]() ;
;
②∵BN=2AN,
∴AN=2,BN=4,
由(1)证得∠BAF=∠AMN,∵∠ABF=∠MAN=90°,
∴△ABF∽△AMN,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴BF= ![]() ,
,
由①求得BF= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t=2,
∴BF=3,
∴FN= ![]() =5
=5
【解析】(1)根据四边形的性质得到AD=AB,∠BAD=90°,由垂直的定义得到∠AHM=90°,由余角的性质得到∠BAF=∠AMH,根据全等三角形的性质即可得到结论;(2)①根据勾股定理得到BD=6 ![]() ,由题意得,DM=t,BE=
,由题意得,DM=t,BE= ![]() t,求得AM=6﹣t,DE=6
t,求得AM=6﹣t,DE=6 ![]() ﹣
﹣ ![]() t,根据相似三角形的判定和性质即可得到结论;②根据已知条件得到AN=2,BN=4,根据相似三角形的性质得到BF=
t,根据相似三角形的判定和性质即可得到结论;②根据已知条件得到AN=2,BN=4,根据相似三角形的性质得到BF= ![]() ,由①求得BF=
,由①求得BF= ![]() ,得方程
,得方程 ![]() =
= ![]() ,于是得到结论.
,于是得到结论.
【考点精析】掌握全等三角形的性质和勾股定理的概念是解答本题的根本,需要知道全等三角形的对应边相等; 全等三角形的对应角相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年5月,某大型商业集团随机抽取所属的部分商业连锁店进行评估,将抽取的各商业连锁店按照评估成绩分成了A、B、C、D四个等级,并绘制了如图不完整的扇形统计图和条形统计图.
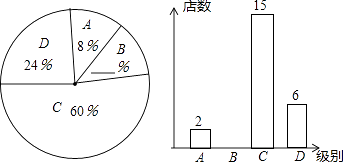
根据以上信息,解答下列问题:
(1)本次评估随即抽取了多少甲商业连锁店?
(2)请补充完整扇形统计图和条形统计图,并在图中标注相应数据;
(3)从A、B两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】双峰县教育局要求各学校加强对学生的安全教育,全县各中小学校引起高度重视,小刚就本班同学对安全知识的了解程度进行了一次调查统计.他将统计结果分为三类,A:熟悉;B:了解较多;C:一般了解。图①和图②是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求小刚所在的班级共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整‘’
(3)在扇形统计图中,计算“了解较多”部分所对应的扇形圆心角的度数;
(4)如果小刚所在年级共1000名同学,请你估算全年级对安全知识“了解较多”的学生人数.
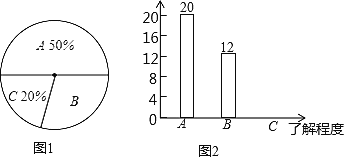
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.

(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PCPA;
(3)当AC=6,CP=3时,求sin∠PAB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度,已知动点A、B的速度比为1:3(速度单位:1个单位长度秒).

(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,满足OB=2OA?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标分别是( )

A. (2,2),(3,4),(1,7) B. (2,2),(4,3),(1,7)
C. (-2,2),(3,4),(1,7) D. (2,-2),(4,3),(1,7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(3,2).点D、E分别在AB、BC边上,BD=BE=1.沿直线DE将△BDE翻折,点B落在点B′处.则点B′的坐标为_____.
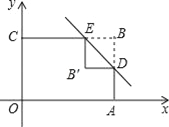
相关试题

