【题目】如图,已知△ABC和△DEF是两个边长都为8cm的等边三角形,且 B、D、C、F都在同一条直线上,连接AD、CE
(1)求证:四边形ADEC是平行四边形
(2)若BD=3cm, △ABC沿着BF的方向以每秒1cm的速度运动,设△ABC运动时间为t秒
①当t等于多少秒时,四边形ADEC为菱形;
②点B运动过程中,四边形ADEC有可能是矩形吗?若可能,请画出图形,并求出t的值;若不可能,请说明理由.

参考答案:
【答案】(1)证明见解析,(2)①当t=3秒时,ADEC是菱形,②当t=11秒时,四边形ADEC是矩形.图形见解析.
【解析】
(1)因为△ABC和△DEF是两个边长为8cm的等边三角形,所以AC=DF,又∠ACD=∠FDE=60°,可得AC∥DE,所以四边形ADEC是平行四边形;
(2)①根据有一组邻边相等的四边形是菱形即可得到结论;
②根据有一个角是直角的平行四边形是矩形即可得到结论.
(1)证明:∵△ABC和△DEF是两个边长为8cm的等边三角形.
∴AC=DE,∠ACD=∠FDE=60°,
∴AC∥DE,
∴四边形ADEC是平行四边形.
(2)解:①当t=3秒时,ADEC是菱形,
∵当t=3秒时,此时B与D重合,∴AD=DE,
∴ADEC是菱形,
②若平行四边形ADEC是矩形,则∠ADE=90°

∴∠ADC=90°-60°=30°
同理∠DAB=30°=∠ADC,
∴BA=BD,
同理FC=EF,
∴F与B重合,
∴t=(8+3)÷1=11秒,
∴当t=11秒时,四边形ADEC是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线形状如图(1)所示.图(2)建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系是
 .请回答下列问题:
.请回答下列问题:
(1)柱子OA的高度是多少米?
(2)喷出的水流距水平面的最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米才能使喷出的水流不至于落在池外?
-
科目: 来源: 题型:
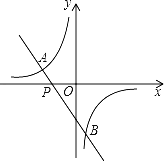
查看答案和解析>>【题目】已知:如图,一次函数y=﹣2x﹣3的图象与反比例函数y=
 (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,O是对角线AC的中点,过O作AC的垂线与边AD、BC分别交于E、F。
(1)求证:四边形AFCE是菱形;
(2)若AF⊥BC,试猜想四边形AFCE是什么特殊四边形,并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是正方形ABCD的边AB上的动点,但始终保持EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF;
(2)若正方形的边长为4,设AE=x,BF=y,求y与x之间的函数解析式;
(3)当x取何值时,y有最大值?并求出这个最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数y=x2+bx+c的图象过点A(1,0)和C(0,﹣3)
(1)求这个二次函数的解析式;
(2)如果这个二次函数的图象与x轴的另一个交点为B,求线段AB的长.
(3)在这条抛物线上是否存在一点P,使△ABP的面积为8?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=________.

相关试题

